
题目列表(包括答案和解析)
已知函数 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)设 ,若对任意
,若对任意 ,
, ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【解析】第一问利用 的定义域是
的定义域是

由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
第二问中,若对任意 不等式
不等式 恒成立,问题等价于
恒成立,问题等价于 只需研究最值即可。
只需研究最值即可。
解: (I) 的定义域是
的定义域是 ......1分
......1分
 ............. 2分
............. 2分
由x>0及 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3,
故函数 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是 ........4分
........4分
(II)若对任意 不等式
不等式 恒成立,
恒成立,
问题等价于 ,
.........5分
,
.........5分
由(I)可知,在 上,x=1是函数极小值点,这个极小值是唯一的极值点,
上,x=1是函数极小值点,这个极小值是唯一的极值点,
故也是最小值点,所以 ; ............6分
; ............6分

当b<1时, ;
;
当 时,
时, ;
;
当b>2时, ;
............8分
;
............8分
问题等价于
 ........11分
........11分
解得b<1 或 或
或  即
即 ,所以实数b的取值范围是
,所以实数b的取值范围是
已知函数 ,
, .
.
(Ⅰ)若函数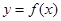 依次在
依次在 处取到极值.求
处取到极值.求 的取值范围;
的取值范围;
(Ⅱ)若存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式
 恒成立.求正整数
恒成立.求正整数 的最大值.
的最大值.
【解析】第一问中利用导数在在 处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中,利用存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式
 恒成立转化为
恒成立转化为 ,恒成立,分离参数法求解得到范围。
,恒成立,分离参数法求解得到范围。
解:(1)
①

(2)不等式  ,即
,即 ,即
,即 .
.
转化为存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式 恒成立.
恒成立.
即不等式 在
在 上恒成立.
上恒成立.
即不等式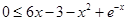 在
在 上恒成立.
上恒成立.
设 ,则.
,则.
设 ,则
,则 ,因为
,因为 ,有
,有 .
.
故 在区间
在区间 上是减函数。又
上是减函数。又
故存在 ,使得
,使得 .
.
当 时,有
时,有 ,当
,当 时,有
时,有 .
.
从而 在区间
在区间 上递增,在区间
上递增,在区间 上递减.
上递减.
又 [来源:]
[来源:]

所以当 时,恒有
时,恒有 ;当
;当 时,恒有
时,恒有
 ;
;
故使命题成立的正整数m的最大值为5
(本小题满分14分)
设函数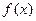 定义在
定义在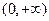 上,
上,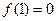 ,导函数
,导函数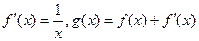
(Ⅰ)求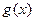 的单调区间的最小值;(Ⅱ)讨论
的单调区间的最小值;(Ⅱ)讨论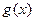 与
与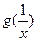 的大小关系;(Ⅲ)是否存在
的大小关系;(Ⅲ)是否存在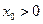 ,使得
,使得 对任意
对任意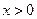 成立?若存在,求出
成立?若存在,求出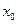 的取值范围;若不存在请说明理由。
的取值范围;若不存在请说明理由。
已知函数 ,
, .
.
(Ⅰ)若函数 和函数
和函数 在区间
在区间 上均为增函数,求实数
上均为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 有唯一解,求实数
有唯一解,求实数 的值.
的值.
【解析】第一问, 
当0<x<2时, ,当x>2时,
,当x>2时, ,
,
要使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须

如使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须 ,即
,即
由上得出,当 时
时 ,
, 在
在 上均为增函数
上均为增函数
(Ⅱ)中方程 有唯一解
有唯一解 有唯一解
有唯一解
设 (x>0)
(x>0)
 随x变化如下表
随x变化如下表
|
x |
|
|
|
|
|
- |
|
+ |
|
|
|
极小值 |
|
由于在 上,
上, 只有一个极小值,
只有一个极小值,
 的最小值为-24-16ln2,
的最小值为-24-16ln2,
当m=-24-16ln2时,方程 有唯一解得到结论。
有唯一解得到结论。
(Ⅰ)解:
当0<x<2时, ,当x>2时,
,当x>2时, ,
,
要使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须

如使 在(a,a+1)上递增,必须
在(a,a+1)上递增,必须 ,即
,即
由上得出,当 时
时 ,
, 在
在 上均为增函数 ……………6分
上均为增函数 ……………6分
(Ⅱ)方程 有唯一解
有唯一解 有唯一解
有唯一解
设 (x>0)
(x>0)
 随x变化如下表
随x变化如下表
|
x |
|
|
|
|
|
- |
|
+ |
|
|
|
极小值 |
|
由于在 上,
上, 只有一个极小值,
只有一个极小值,
 的最小值为-24-16ln2,
的最小值为-24-16ln2,
当m=-24-16ln2时,方程 有唯一解
有唯一解
(本题满分14分)
已知函数![]() 。
。
(1)求![]() 的最大值及取得最大值时的
的最大值及取得最大值时的![]() 的值;
的值;
(2)求![]() 在
在![]() 上的单调增区间。
上的单调增区间。
一、选择题:本大题共8个小题,每小题5分,共40分。
题号
1
2
3
4
5
6
7
8
答案
B
A
B
D
C
D
C
D
二、填空题:本大题共6个小题,每小题5分,共30分
9.数学文科.files/image197.gif) 10. 60
10. 60数学文科.files/image199.gif) 11.
11.数学文科.files/image201.gif) 12.
12.数学文科.files/image203.gif) 13. 2 14. -2;1
13. 2 14. -2;1
三、解答题: 本大题共6个小题,共80分。
15. (本小题共13分)
已知函数数学文科.files/image111.gif)
(Ⅰ)求函数数学文科.files/image056.gif) 的定义域;
的定义域;
(Ⅱ)求函数数学文科.files/image056.gif) 在区间
在区间数学文科.files/image115.gif) 上的最值。
上的最值。
解:(Ⅰ)由题意 数学文科.files/image206.gif)
数学文科.files/image208.gif)
数学文科.files/image210.gif)
所求定义域为 {数学文科.files/image212.gif) }
…………4分
}
…………4分
(Ⅱ)数学文科.files/image214.gif)
数学文科.files/image216.gif)
数学文科.files/image218.gif)
数学文科.files/image220.gif) …………9分
…………9分
由数学文科.files/image222.gif) 知
知 数学文科.files/image224.gif) ,
,
所以当数学文科.files/image226.gif) 时,
时,数学文科.files/image056.gif) 取得最大值为
取得最大值为数学文科.files/image228.gif) ;
…………11分
;
…………11分
当数学文科.files/image230.gif) 时,
时,数学文科.files/image056.gif) 取得最小值为0 。
…………13分
取得最小值为0 。
…………13分
16. (本小题共13分)
已知数列数学文科.files/image117.gif) 中,
中,数学文科.files/image119.gif) ,点(1,0)在函数
,点(1,0)在函数数学文科.files/image121.gif) 的图像上。
的图像上。
(Ⅰ)求数列数学文科.files/image123.gif) 的通项;
的通项;
(Ⅱ)设数学文科.files/image125.gif) ,求数列
,求数列数学文科.files/image127.gif) 的前n项和
的前n项和数学文科.files/image129.gif) 。
。
解:(Ⅰ)由已知 数学文科.files/image232.gif) 又
又数学文科.files/image234.gif)
数学文科.files/image236.gif) …………3分
…………3分
所以 数列数学文科.files/image123.gif) 是公比为
是公比为数学文科.files/image070.gif) 的等比数列 所以
的等比数列 所以 数学文科.files/image239.gif) …………6分
…………6分
(Ⅱ) 由 数学文科.files/image241.gif) …………9分
…………9分
所以
数学文科.files/image243.gif) …………13分
…………13分
17. (本小题共14分)
数学文科.files/image131.gif) 如图,在正三棱柱
如图,在正三棱柱数学文科.files/image133.gif) 中,
中,数学文科.files/image135.gif) ,
,数学文科.files/image137.gif) 是
是数学文科.files/image139.gif) 的中点,点
的中点,点数学文科.files/image141.gif) 在
在数学文科.files/image143.gif) 上,
上,数学文科.files/image145.gif) 。
。
(Ⅰ)求数学文科.files/image147.gif) 所成角的大小;
所成角的大小;
(Ⅱ)求二面角数学文科.files/image149.gif) 的正切值;
的正切值;
(Ⅲ) 证明数学文科.files/image151.gif) .
.
解:(Ⅰ)在正三棱柱数学文科.files/image133.gif) 中,
中, 数学文科.files/image245.gif)
数学文科.files/image247.gif)
数学文科.files/image249.gif)
又 数学文科.files/image137.gif) 是正△ABC
是正△ABC数学文科.files/image139.gif) 边的中点,
边的中点,数学文科.files/image247.gif)
数学文科.files/image252.gif)
数学文科.files/image234.gif)
数学文科.files/image254.gif)
数学文科.files/image247.gif)
数学文科.files/image256.gif) …………3分
…………3分
数学文科.files/image247.gif) ∠
∠数学文科.files/image258.gif) 为
为数学文科.files/image147.gif) 所成角
所成角
又 数学文科.files/image260.gif)
数学文科.files/image261.gif) sin∠
sin∠数学文科.files/image258.gif) =
=数学文科.files/image264.gif) …………5分
…………5分
所以数学文科.files/image147.gif) 所成角为
所成角为数学文科.files/image266.gif) (
(数学文科.files/image268.gif) )
)
(Ⅱ) 由已知得 数学文科.files/image270.gif)
∠数学文科.files/image272.gif) 为二面角
为二面角数学文科.files/image149.gif) 的平面角, 所以
的平面角, 所以 数学文科.files/image274.gif) …………9分
…………9分
(Ⅲ)证明: 依题意 得 数学文科.files/image276.gif) ,
,数学文科.files/image278.gif) ,
,数学文科.files/image280.gif)
因为 数学文科.files/image282.gif)
数学文科.files/image283.gif)
数学文科.files/image285.gif)
数学文科.files/image287.gif) …………11分
…………11分
又由(Ⅰ)中数学文科.files/image256.gif) 知
知数学文科.files/image289.gif) ,且
,且数学文科.files/image287.gif)
数学文科.files/image291.gif) ,
,
数学文科.files/image283.gif)
数学文科.files/image293.gif)
数学文科.files/image151.gif) …………14分
…………14分
18. (本小题共13分)
某校高二年级开设《几何证明选讲》及《数学史》两个模块的选修科目。每名学生至多选修一个模块,数学文科.files/image153.gif) 的学生选修过《几何证明选讲》,
的学生选修过《几何证明选讲》,数学文科.files/image155.gif) 的学生选修过《数学史》,假设各人的选择相互之间没有影响。
的学生选修过《数学史》,假设各人的选择相互之间没有影响。
(Ⅰ)任选1名学生,求该生没有选修过任何一个模块的概率;
(Ⅱ)任选4名学生,求至少有3人选修过《几何证明选讲》的概率。
解:(Ⅰ)设该生参加过《几何证明选讲》的选修为事件A,
参加过《数学史》的选修为事件B, 该生没有选修过任何一个模块的概率为P,
则数学文科.files/image295.gif)
所以 该生没有选修过任何一个模块的概率为数学文科.files/image297.gif) …………6分
…………6分
(Ⅱ)至少有3人选修过《几何证明选讲》的概率为
数学文科.files/image299.gif)
所以至少有3人选修过《几何证明选讲》的概率为数学文科.files/image301.gif) …………13分
…………13分
数学文科.files/image302.jpg) 19. (本小题共13分)
19. (本小题共13分)
已知函数数学文科.files/image159.gif) 的图像如图所示。
的图像如图所示。
(Ⅰ)求数学文科.files/image161.gif) 的值;
的值;
(Ⅱ)若函数数学文科.files/image056.gif) 在
在数学文科.files/image164.gif) 处的切线方程为
处的切线方程为数学文科.files/image166.gif) ,求函数
,求函数数学文科.files/image056.gif) 的
的
解析式;
(Ⅲ)若数学文科.files/image168.gif) =5,方程
=5,方程数学文科.files/image170.gif) 有三个不同的根,求实数
有三个不同的根,求实数数学文科.files/image172.gif) 的取值范围。
的取值范围。
解: 函数数学文科.files/image056.gif) 的导函数为
的导函数为 数学文科.files/image304.gif)
(Ⅰ)由图可知
函数数学文科.files/image056.gif) 的图像过点(0,3),且
的图像过点(0,3),且数学文科.files/image306.gif)
得 数学文科.files/image308.gif) …………3分
…………3分
(Ⅱ)依题意
数学文科.files/image310.gif) 且
且数学文科.files/image312.gif)
数学文科.files/image314.gif) 解得
解得 数学文科.files/image316.gif)
所以数学文科.files/image318.gif) …………8分
…………8分
(Ⅲ)依题意 数学文科.files/image320.gif)
由 数学文科.files/image322.gif) ①
①
若方程数学文科.files/image170.gif) 有三个不同的根,当且仅当 满足
有三个不同的根,当且仅当 满足 数学文科.files/image324.gif) ②
②
由 ① ② 得 数学文科.files/image326.gif)
所以 当 数学文科.files/image328.gif) 时 ,方程
时 ,方程数学文科.files/image170.gif) 有三个不同的根。 …………13分
有三个不同的根。 …………13分
20. (本小题共14分)
已知数学文科.files/image174.gif) 分别为椭圆
分别为椭圆数学文科.files/image176.gif) 的左、右焦点,直线
的左、右焦点,直线数学文科.files/image178.gif) 过点
过点数学文科.files/image180.gif) 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线数学文科.files/image182.gif) 垂直于直线
垂直于直线数学文科.files/image178.gif) ,垂足为
,垂足为数学文科.files/image184.gif) ,线段
,线段数学文科.files/image186.gif) 的垂直平分线交
的垂直平分线交数学文科.files/image188.gif) 于点M。
于点M。
(Ⅰ)求动点M的轨迹数学文科.files/image190.gif) 的方程;
的方程;
(Ⅱ)过点数学文科.files/image180.gif) 作直线交曲线
作直线交曲线数学文科.files/image190.gif) 于两个不同的点P和Q,设=
于两个不同的点P和Q,设=数学文科.files/image192.gif) ,若
,若数学文科.files/image192.gif) ∈[2,3],求
∈[2,3],求数学文科.files/image195.gif) 的取值范围。
的取值范围。
解:(Ⅰ)设M数学文科.files/image330.gif) ,则
,则数学文科.files/image332.gif) ,由中垂线的性质知
,由中垂线的性质知数学文科.files/image334.gif)
数学文科.files/image283.gif) |
|数学文科.files/image336.gif) |=
|=数学文科.files/image338.gif) 化简得
化简得数学文科.files/image190.gif) 的方程为
的方程为数学文科.files/image340.gif) …………3分
…………3分
(另:由数学文科.files/image334.gif) 知曲线
知曲线数学文科.files/image190.gif) 是以x轴为对称轴,以
是以x轴为对称轴,以数学文科.files/image343.gif) 为焦点,以
为焦点,以数学文科.files/image178.gif) 为准线的抛物线
为准线的抛物线
所以 数学文科.files/image345.gif) ,
则动点M的轨迹
,
则动点M的轨迹数学文科.files/image190.gif) 的方程为
的方程为数学文科.files/image340.gif) )
)
(Ⅱ)设数学文科.files/image347.gif) ,由=
,由=数学文科.files/image192.gif) 知
知 数学文科.files/image349.gif) ①
①
又由数学文科.files/image347.gif) 在曲线
在曲线数学文科.files/image190.gif) 上知
上知 数学文科.files/image351.gif) ②
②
由 ① ② 解得数学文科.files/image353.gif) 所以
有
所以
有 数学文科.files/image355.gif) …………8分
…………8分
数学文科.files/image283.gif)
数学文科.files/image195.gif) =
=数学文科.files/image357.gif) =
=数学文科.files/image359.gif) =
=数学文科.files/image361.gif) …………10分
…………10分
设数学文科.files/image363.gif) ,
,数学文科.files/image192.gif) ∈[2,3],
有
∈[2,3],
有数学文科.files/image365.gif) 在区间
在区间数学文科.files/image367.gif) 上是增函数,
上是增函数,
得 数学文科.files/image369.gif) 进而有
进而有 数学文科.files/image371.gif)
所以 数学文科.files/image195.gif) 的取值范围是
的取值范围是数学文科.files/image373.gif) …………14分
…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com