练习册

  • 练习册
  • 试题
    已知数列中..点(1.0)在函数的图像上. 【查看更多】

     

    题目列表(包括答案和解析)

    已知数列满足

    （1）求数列的通项公式；

    （2）设b= (n∈N，n≥2), b,

           求证：b1+b2……+bn< 3；

    （3）设点M(n,b)((n∈N，n>2)在这些点中是否存在两个不同的点同时在函数

    y =(k>0)的图象上,如果存在,求出点的坐标,若不存在,请说明理由.

    查看答案和解析>>

    已知数列{an}的前n项和为Sn,点（n,an）(n∈N*)在函数f(x)=-2x-2的图象上，数列{bn}的前n项和为Tn,且Tn是6Sn与8n的等差中项.

    (1)求数列{bn}的通项公式;

    (2)设cn=bn+8n+3,数列{dn}满足d1=c1,dn+1=cdn(n∈N*).求数列{dn}的前n项和Dn;

    (3)设g(x)是定义在正整数集上的函数,对于任意的正整数x1,x2恒有g(x1x2)=x1g(x2)+x2g(x1)成立,且g(2)=a(a为常数,a≠0),试判断数列{}是否为等差数列,并说明理由.

    查看答案和解析>>

    已知数列{an}中，a1=1，且点P（an，an+1）（n∈N*）在直线x-y+1=0上．
    （1）求数列{an}的通项公式；
    （2）若函数f（n）=
    1
    n+a1
    +
    1
    n+a2
    +
    1
    n+a3
    +…+
    1
    n+an
    （n∈N*，且n≥2），求函数f（n）的最小值．

    查看答案和解析>>

    已知数列{an}中，a1=
    1
    2
    ，点（1，0）在函数f(x)=
    1
    2
    anx2-an+1x    的图象上．
    （Ⅰ）求数列{an}的通项；
    （Ⅱ）设bn=log2a2n-1，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    已知数列{an}中，a1=1，且点P（an，an+1）在直线x-y+1=0上。
    （1）求数列{an}的通项公式；
    （2）若函数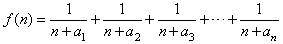（n∈N，且n≥2），求函数f（n）的最小值；
    （3）设bn=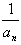，Sn表示数列{bn}的前n项和。试问：是否存在关于n的整式g（n），使得S1+S2+S3+…+Sn-1=（Sn-1）·g（n）对于一切不小于2的自然数n恒成立？ 若存在，写出g（n）的解析式，并加以证明；若不存在，试说明理由。

    查看答案和解析>>

    一、选择题：本大题共8个小题，每小题5分，共40分。

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    答案

    B

    A

    B

    D

    C

    D

    C

    D

    二、填空题：本大题共6个小题，每小题5分，共30分

    9．    10. 60   11.    12.    13. 2    14. -2；1

    三、解答题： 本大题共6个小题，共80分。

    15. （本小题共13分）

    已知函数

    （Ⅰ）求函数的定义域；

    （Ⅱ）求函数在区间上的最值。

    解：（Ⅰ）由题意                 

    所求定义域为  {}                            …………4分

    （Ⅱ）

                               …………9分

    由   知   ，

    所以当时，取得最大值为；                   …………11分

    当时，取得最小值为0 。                   …………13分

    16. （本小题共13分）

    已知数列中，，点（1，0）在函数的图像上。

    （Ⅰ）求数列 的通项；

    （Ⅱ）设，求数列的前n项和。      

    解：(Ⅰ)由已知        又         …………3分

     所以 数列是公比为的等比数列      所以        …………6分

         （Ⅱ） 由                                …………9分

          所以                …………13分

    17. （本小题共14分）

    如图，在正三棱柱中，,是的中点，点在上，。

    （Ⅰ）求所成角的大小；        

    （Ⅱ）求二面角的正切值；

    (Ⅲ) 证明.

    解：（Ⅰ）在正三棱柱中，  

    又  是正△ABC边的中点，

                                   …………3分

    ∠为所成角

    又     sin∠=                      …………5分

    所以所成角为（）

    （Ⅱ） 由已知得 

       ∠为二面角的平面角，     所以     …………9分

    (Ⅲ)证明:  依题意  得   ，，

    因为                        …………11分

    又由（Ⅰ）中    知，且，

                                          …………14分

    18. （本小题共13分）

    某校高二年级开设《几何证明选讲》及《数学史》两个模块的选修科目。每名学生至多选修一个模块，的学生选修过《几何证明选讲》，的学生选修过《数学史》，假设各人的选择相互之间没有影响。

    (Ⅰ)任选1名学生，求该生没有选修过任何一个模块的概率；

    (Ⅱ)任选4名学生，求至少有3人选修过《几何证明选讲》的概率。

    解：(Ⅰ)设该生参加过《几何证明选讲》的选修为事件A，

    参加过《数学史》的选修为事件B， 该生没有选修过任何一个模块的概率为P，

    则

    所以 该生没有选修过任何一个模块的概率为                     …………6分

    (Ⅱ)至少有3人选修过《几何证明选讲》的概率为

           

      所以至少有3人选修过《几何证明选讲》的概率为               …………13分

    19. （本小题共13分）

    已知函数的图像如图所示。

    (Ⅰ)求的值；

    (Ⅱ)若函数在处的切线方程为，求函数的        

    解析式；

    （Ⅲ）若=5，方程有三个不同的根，求实数的取值范围。

      解： 函数的导函数为  

    (Ⅰ)由图可知  函数的图像过点（0，3），且

      得                         …………3分

    (Ⅱ)依题意  且

             解得  

       所以                                 …………8分

    （Ⅲ）依题意

              由                                       ①

        若方程有三个不同的根，当且仅当 满足        ②

      由 ① ②  得   

       所以 当  时 ，方程有三个不同的根。     …………13分

    20. （本小题共14分）

           已知分别为椭圆的左、右焦点，直线过点且垂直于椭圆的长轴，动直线垂直于直线，垂足为，线段的垂直平分线交于点M。

    (Ⅰ)求动点M的轨迹的方程；

    (Ⅱ)过点作直线交曲线于两个不同的点P和Q，设＝，若∈[2，3]，求的取值范围。

    解：(Ⅰ)设M，则，由中垂线的性质知

    ||=     化简得的方程为                  …………3分

    （另：由知曲线是以x轴为对称轴，以为焦点，以为准线的抛物线

        所以  ，         则动点M的轨迹的方程为）

    (Ⅱ)设，由＝  知        ①

    又由 在曲线上知                   ②

    由  ①  ②       解得    所以 有          …………8分

     ===  …………10分

    设 ，∈[2，3]， 有 在区间上是增函数，

    得       进而有      

    所以    的取值范围是                             …………14分

                   

     

     

     

     

     

     


    同步练习册答案