
题目列表(包括答案和解析)
以下七个命题:
(1)垂直于同一条直线的两个平面平行;
(2)平行于同一条直线的两个平面平行;
(3)平行于同一个平面的两个平面平行;
(4)一个平面内的两相交直线与另一个平面内的两条相交直线平行,则这两个平面平行;
(5)与同一条直线成等角的两个平面平行;
(6)一个平面上不共线三点到另一平面的距离相等;
(7)两个平面分别与第三个平面相交所得的两条交线平行,则这两个平面平行.
其中正确命题的序号是________.
(10分)某运动员射击一次所得环数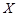 的分布如下:
的分布如下:
|
|
0~6 |
7 |
8 |
9 |
10 |
|
|
0 |
|
|
|
|
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为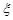 .
.
(I)求该运动员两次都命中7环的概率
(II)求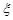 的分布列
的分布列
(III)求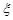 的数学期望
的数学期望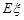
| π |
| 3 |
| π |
| 6 |
| x2 |
| 9 |
| y2 |
| 4 |
 ,求随机变量
,求随机变量 的分布列和期望
的分布列和期望 以及方差
以及方差
从以下两个小题中选做一题(只能做其中一个,做两个按得分最低的记分).(甲)一水池有2个进水口,1个出水口,每口进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)

给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则一定能确定正确的论断序号是________.
(乙)深圳市的一种特色水果上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格连续下跌,现有三种价格模拟函数.①f(x)p·qx;②f(x)=px2+qx+1;③f(x)=x(x-q)2+p
(以上三式中p,q均为常数,且q>1,x=0表示4月1日,x=1表示5月1日,依次类推).
(1)为准确研究其价格走势,应选________种价格模拟函数.
(2)若f(x)=4,f(2)=6,预测该果品在________月份内价格下跌.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com