
题目列表(包括答案和解析)
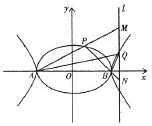 已知A,B分别是椭圆C1:
已知A,B分别是椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 5 |
| 2 |
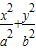 =1的左、右顶点,P是椭圆上异与A,B的任意一点,Q是双曲线C2:
=1的左、右顶点,P是椭圆上异与A,B的任意一点,Q是双曲线C2: =1上异与A,B的任意一点,a>b>0.
=1上异与A,B的任意一点,a>b>0.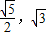 ),Q(
),Q( ,1),求椭圆Cl的方程;
,1),求椭圆Cl的方程;
如图,将一张矩形的纸对折以后略微展开,竖立在桌面上,说明折痕为什么与桌面垂直.

从图中可直观地看出,折痕垂直于对折后的纸与桌面所形成的交线.由直线与平面垂直的判定定理知,折痕与桌面垂直.那么在折痕垂直于纸与桌面的交线未知的情况下,单凭折后的纸与桌面垂直,能否得出折痕与桌面垂直?转化为数学语言,即如果两个相交平面都垂直于第三个平面,那么它们的交线也垂直于第三个平面吗?下面用不同的方法证明.
如图,已知平面α⊥平面β,平面α⊥平面γ,且β∩γ=a,β∩α=l,γ∩α=m.

求证:a⊥α.
在棱长为 的正方体
的正方体 中,
中, 是线段
是线段 的中点,
的中点, .
.
(1) 求证: ^
^ ;
;
(2) 求证: //平面
//平面 ;
;
(3) 求三棱锥 的表面积.
的表面积.

【解析】本试题考查了线线垂直和线面平行的判定定理和表面积公式的运用。第一问中,利用 ,得到结论,第二问中,先判定
,得到结论,第二问中,先判定 为平行四边形,然后
为平行四边形,然后 ,可知结论成立。
,可知结论成立。
第三问中, 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
,
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为 .
.
解: (1)证明:根据正方体的性质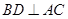 ,
,
因为 ,
,
所以 ,又
,又 ,所以
,所以 ,
, ,
,
所以 ^
^ .
………………4分
.
………………4分
(2)证明:连接 ,因为
,因为 ,
,
所以 为平行四边形,因此
为平行四边形,因此 ,
,
由于 是线段
是线段 的中点,所以
的中点,所以 , …………6分
, …………6分
因为
 面
面 ,
,
 平面
平面 ,所以
,所以 ∥平面
∥平面 . ……………8分
. ……………8分
(3) 是边长为
是边长为 的正三角形,其面积为
的正三角形,其面积为 ,
,
因为 平面
平面 ,所以
,所以 ,
,
所以 是直角三角形,其面积为
是直角三角形,其面积为 ,
,
同理 的面积为
的面积为 ,
……………………10分
,
……………………10分
 面积为
面积为 . 所以三棱锥
. 所以三棱锥 的表面积为
的表面积为

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com