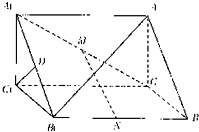如图，直三棱柱ABC-A₁B₁C₁的底面积是等腰直角三角形，∠A₁C₁B₁=90°，A₁C₁=1，AA₁=

2

，N、M分别是线段B₁B、AC₁的中点．
（I）证明：MN∥平面ABC；
（II）求A₁到平面AB₁C₁的距离
（III）求二面角A₁-AB₁-C₁的大小．

查看答案和解析>>

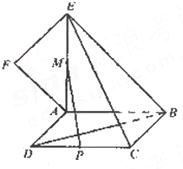如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ABE是等腰直角三角形，AB=AE，FA=FE，∠AEF=45°
（I）求证：EF⊥平面BCE；
（Ⅱ）设线段CD、AE的中点分别为P、M，求证：PM∥平面BCE；
（Ⅲ）求二面角F-BD-A的大小．

查看答案和解析>>

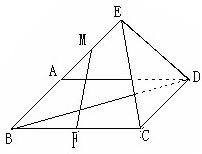如图，正方形ABCD所在的平面与三角形ADE所在平面互相垂直，△AEB是等腰直角三角形，且AE=ED设线段BC、PBC的中点分别为F、M，
求证：（1）FM∥平面ECD；
（2）求二面角E-BD-A的正切值．

查看答案和解析>>

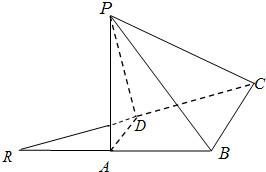如图，已知等腰直角三角形RBC，其中∠RBC=90°，RB=BC=2．点A、D分别是RB、RC的中点，现将△RAD沿着边AD折起到△PAD位置，使PA⊥AB，连接PB、PC．
（1）求证：BC⊥PB；
（2）求二面角A-CD-P的平面角的余弦值．

查看答案和解析>>

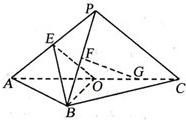如图，平面PAC⊥平面ABC，△ABC是以AC为斜边的等腰直角三角形，E、F、O分别为PA，PB，AC的中点，AC=16，PA=PC=10．
（I）设G是OC的中点，证明：FG∥平面BOE；
（II）证明：在△ABO内存在一点M，使FM⊥平面BOE．

查看答案和解析>>

一．选择题：ABCDC CAACB

解析：

1： M，P表示元素分别为直线和圆的两个集合，它们没有公共元素。故选A。

2：因，取α=－代入sinα>tanα>cotα，满足条件式，则排除A、C、D，故选B。

3：构造特殊函数f(x)=x，虽然满足题设条件，并易知f(x)在区间[－7，－3]上是增函数，且最大值为f(-3)=-5，故选C。

4：题中可写成。联想数学模型：过两点的直线的斜率公式k=，可将问题看成圆(x－2)²+y²=3上的点与坐标原点O连线的斜率的最大值，即得D。

5：因纬线弧长＞球面距离＞直线距离，排除A、B、D，故选C。

6：取满足题意的特殊数列，则，故选C。

7：二项式中含有，似乎增加了计算量和难度，但如果设，，则待求式子。故选A。

8：去掉题中的修饰语，本题的实质就是学生所熟悉的这样一个题目：三男三女站成一排，男女相间而站，问有多少种站法？因而易得本题答案为。故选A。

9：考虑特殊位置PQ⊥OP时，，所以，故选C。

10：08年农民工次性人均收入为：

又08年农民其它人均收入为1350+160=2150

故08年农民人均总收入约为2405+2150=4555（元）。故选B。

二．填空题：11.25;    12. ;  13.  _{， ；}14.；  15、；

解析：11：

12：

13：；

14.解：由，得

15．解：∵PA切于点A，B为PO中点，∴AB=OB=OA, ∴,∴,

在△POD中由余弦定理 ，得=

∴

三．解答题：

16.解：（Ⅰ）∵

∴     ∴-----------------2分

若则得----------------------------4分

∵  

∴或

∴ -------------------------------------------------6分

（Ⅱ）∵

＝

----------------------------------9分

   ∴函数的最小正周期为T=π-----------------------------------------10分

由得

∴的单调增区间.----------------12分

17．（Ⅰ）证法一：在中，是等腰直角的中位线，

                              ……………………………1分

在四棱锥中，，，       ……………2分

平面，                                        ……5分

又平面,                           …………7分

证法二：同证法一                              …………2分

                                    ……………………4分

平面，                                      ………5分

又平面,                  ……………………7分

（Ⅱ）在直角梯形中，

,                     ……8分

又垂直平分，           ……10分

三棱锥的体积为：

                ………12分

18．解：由题意可知,图甲图象经过（1,1）和（6,2）两点,

从而求得其解析式为y_甲=0.2x+0.8-----------------------（2分）

图乙图象经过（1,30）和（6,10）两点,

从而求得其解析式为y_乙=-4x+34.------------------------- （4分）

(Ⅰ)当x=2时，y_甲=0.2×2+0.8 =1.2,y_乙= -4×2+34=26，

y_甲?y_乙=1.2×26=31.2.

所以第2年鱼池有26个,全县出产的鳗鱼总数为31.2万只.------------ ---（6分）

 (Ⅱ)第1年出产鱼1×30=30（万只）, 第6年出产鱼2×10=20（万只）,可见,第6年这个县的鳗鱼养殖业规划比第1年缩小了----------------------------------（8分）

 (Ⅲ)设当第m年时的规模总出产量为n,

那么n=y_甲?y_乙=（0.2m+0.8） (-4m+34)= -0. 8m²+3.6m+27.2

      =-0.8(m²-4.5m-34)=-0.8(m-2.25)²+31.25---------------------------（11分）

因此, .当m=2时,n最大值=31.2.

即当第2年时,鳗鱼养殖业的规模最大,最大产量为31.2万只. --------------（14分）

19．解：(Ⅰ) 由得: ,……（2分）

变形得: 即:, ………（４分）

数列是首项为1,公差为的等差数列. ………（5分）

(Ⅱ) 由(1)得:, ………（7分）

, ………（9分）

（Ⅲ）由(1)知:  ………(11分）

………（1４分）

20．解：（Ⅰ）由题意知，动圆圆心Q到点A和到定直线的距离相等，

∴动圆圆心Q的轨迹是以点A为焦点，以直线为准线的抛物线

∴曲线C的方程为。 -------------------------------------------------4分

（Ⅱ）如图，设点，则的坐标为，

，∴曲线C在点处的切线方程为： -----------7分

令y＝0，得此切线与x轴交点的横坐标，即， ， ---------10分

∴

∴数列是首项公比为的等比数列， -----12分

 -------------14分

21．解：（Ⅰ）令

得……………………………………2分

当时，　  　故在上递减．

当    故在上递增．

所以，当时，的最小值为….……………………………………..4分

（Ⅱ）由，有　即

故　．………………………………………5分

（Ⅲ）证明:要证：

只要证：

 设…………………7分

则

令得…………………………………………………….8分

当时，

故上递减，类似地可证递增

所以的最小值为………………10分

而=

=

=

由定理知:  故

故

即: .…………………………..14分