
题目列表(包括答案和解析)
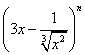 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中(A)7 (B)![]() (C)21 (D)
(C)21 (D)![]()
 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中(A)7 (B)![]() (C)21 (D)
(C)21 (D)![]()
如果 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中![]() 的系数是( )
的系数是( )
(A)7 (B)-7 (C)21 (D)-21
如果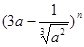 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中 的系数是 ( )
的系数是 ( )
A.-2835 B.2835 C.21 D.-21
如果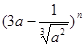 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中 的系数是 ( )
的系数是 ( )
A.-2835 B.2835 C.21 D.-21
一.选择题:DBBCB BCCCC
解析:1:因为 =(2 -│
=(2 -│ │)+
│)+  ,由选择支知│
,由选择支知│ │<2,所以
│<2,所以 的实部为正数,虚部为1,根据这个隐含条件,(A),(B),(C)均可筛去,所以选(D).
的实部为正数,虚部为1,根据这个隐含条件,(A),(B),(C)均可筛去,所以选(D).
2:先将周期最小的选项(A)的周期T= 代入
代入 检验,不成立则排除(A);再检验(B)成立. 所以选(B).
检验,不成立则排除(A);再检验(B)成立. 所以选(B).
3:∵ ∴可取
∴可取 代入四个选项验证,发现B错误,∴应选(B).
代入四个选项验证,发现B错误,∴应选(B).
4:“ 的展开式中各项系数之和为
的展开式中各项系数之和为
由通项公式Tr+1= =
= ,
,
令7-=-3,解得r=6,此时T7= ,故选C

5:作两直线的图象,从图中可以看出:
直线 的倾斜角的取值范围应选(B).
的倾斜角的取值范围应选(B).
6:取特殊数列 =
= ,排除(A)、(C)、(D). ∴选(B).
,排除(A)、(C)、(D). ∴选(B).
7:如图所示,
作
∴柱体体积

 故选C.
故选C.
8:由图象可知,x=1时 =1. 由此可排除(A)、(D);再由周期T=8,可排除(B).
=1. 由此可排除(A)、(D);再由周期T=8,可排除(B).
∴应选(C).
9:利用椭圆的定义可得 故离心率
故离心率 故选C。
故选C。
10:设某人当月工资为1200元或1500元,则其应纳税款分别为:400 5%=20元,500
5%=20元,500 5%+200
5%+200 10%=45元,可排除
10%=45元,可排除 、
、 、
、 .故选
.故选 .
.
二.填空题:11、2; 12、a>0且 ;13、
;13、 ;14、
;14、 ;15、7;
;15、7;
解析:11:因为包含了 任意一个元素
任意一个元素 的三元素集合共
的三元素集合共 个,所以在
个,所以在 中,每个元素都出现了
中,每个元素都出现了 次,所以
次,所以

 ,所以
,所以
 。
。
12:由已知可画出下图,符合题设,故a>0且 。
。
13:设P(x,y),则当 时,点P的轨迹为
时,点P的轨迹为 ,由此可得点P的横坐标
,由此可得点P的横坐标 。
。
又当P在x轴上时, ,点P在y轴上时,
,点P在y轴上时, 为钝角,由此可得点P横坐标的取值范围是:
为钝角,由此可得点P横坐标的取值范围是: ;
;
 14.解:在平面直角坐标系中,曲线
14.解:在平面直角坐标系中,曲线 和
和 分别表示圆
分别表示圆 和直线
和直线 ,易知
,易知 =
=
15.解:  由圆的性质PA
由圆的性质PA =PC?PB,得,PB=12,连接OA并反向延长
=PC?PB,得,PB=12,连接OA并反向延长
交圆于点E,在直角三角形APD中可以求得PD=4,DA=2,故CD=3,
DB=8,J记圆的半径为R,由于ED?DA=CD?DB
因此,(2R-2) ?2=3?8,解得R=7
三.解答题:
16.解:(Ⅰ)∵ ∴
∴ ----①,
----①, ----②
----②
由①得 ------③
------③
在△ABC中,由正弦定理得 =
= ,设
,设
 =
=
则 ,代入③得
,代入③得

∵  ∴
∴ ∴
∴ ,∵
,∵ ∴
∴ ……………………6分
……………………6分
(Ⅱ) ∵ ,由余弦定理得
,由余弦定理得

 ,--④
,--④
由②得 -⑤ 由④⑤得
-⑤ 由④⑤得 ,∴
,∴ =
= . ……………………………12分
. ……………………………12分
17.解:设该观众先答A题所获奖金为 元,先答B题所获奖金为
元,先答B题所获奖金为 元,………………………1分
元,………………………1分
依题意可得 可能取的值为:0,
可能取的值为:0,  ,3
,3 ,
,  的可能取值为:0,2
的可能取值为:0,2 ,3
,3
………………………2分
∵ ,
, ,
, ,
,
∴ ,
………………………6分
,
………………………6分
∵ ,
, ,
, 
∴ ………………………10分
………………………10分
∵
 ∴
∴ ,即
,即
∴该观众应先回答B题所获奖金的期望较大. ……………………………12分
18.解:(Ⅰ)设 ,由
,由 得
得 ,解得
,解得 或
或 ,若
,若 则
则 与
与 矛盾,所以
矛盾,所以 不合舍去。
不合舍去。
即 。---------------------------------------------------------------------------6
。---------------------------------------------------------------------------6
(Ⅱ)圆 即
即 ,其圆心为C(3,-1),半径
,其圆心为C(3,-1),半径 ,
,
∴直线OB的方程为 ,-----------------------------------------------------------------10
,-----------------------------------------------------------------10
设圆心C(3,-1)关于直线 的对称点的坐标为(a,b),则
的对称点的坐标为(a,b),则

解得: ,则所求的圆的方程为
,则所求的圆的方程为 。-----------------------------14
。-----------------------------14
19.(Ⅰ)证明:∵对任意的 ①
①
令 得
得 ②…………1分
②…………1分
令 得
得 ……………………2分
……………………2分
∴ 由②得
由②得
∴函数 为奇函数………………………………3分
为奇函数………………………………3分
(Ⅱ)证明:(1)当n=1时等式显然成立
(2)假设当n=k(k )时等式成立,即
)时等式成立,即 ,…………4分
,…………4分
则当n=k+1时有
 ,由①得
,由①得 ………………6分
………………6分
∵ ∴
∴
∴当n=k+1时,等式成立。
综(1)、(2)知对任意的 ,
, 成立。………………8分
成立。………………8分
(Ⅲ)解:设 ,因函数
,因函数 为奇函数,结合①得
为奇函数,结合①得
 =
= ,……………………9分
,……………………9分
∵
又∵当 时,
时,
∴
 ,∴
,∴
∴函数 在R上单调递减…………………………………………12分
在R上单调递减…………………………………………12分
∴

由(2)的结论得 ,
,
∵ ,∴
,∴ =-2n
=-2n
∵函数 为奇函数,∴
为奇函数,∴
∴
 ,
, =2n。……………………14分
=2n。……………………14分
20.解:(1)如图,将侧面BB
∵CD∥AA1 ∴D为CC1的中点,……………………………2分
在Rt△A1AB2中,由勾股定理得 ,
,
即 解得
解得 ,……………………4分
,……………………4分
∵ ∴
∴ ……………………………………6分
……………………………………6分
(2)设A1B与AB1的交点为O,连结BB2,OD,则 ……………………………7分
……………………………7分
∵ 平面
平面 ,
, 平面
平面 ∴
∴ 平面
平面 ,
,
即在平面A1BD内存在过点D的直线与平面ABC平行 ……………………………9分
(3)连结AD,B1D ∵ ≌
≌ ≌
≌
∴ ∴
∴ ……………………………11分
……………………………11分
∵ ∴
∴ 平面A1ABB1 ……………………………13分
平面A1ABB1 ……………………………13分
又∵ 平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
21.解:(Ⅰ)
 …………………………………………1分
…………………………………………1分
由 得
得 , ………………………………………………2分
, ………………………………………………2分
又 得
得 ……………………………………………………3分
……………………………………………………3分
(Ⅱ) k=
k=
 ,
,
 对任意的
对任意的
 ,即
,即 对任意的
对任意的 恒成立……4分
恒成立……4分
等价于 对任意的
对任意的 恒成立。…………………………5分
恒成立。…………………………5分
令g(x)= ,h(x)=
,h(x)= ,
,
则 ,
, …………………………………………6分
…………………………………………6分
 ,当且仅当
,当且仅当 时“=”成立,
时“=”成立,
 …………7分
…………7分
 h(x)=
h(x)= 在(0,1)上为增函数,
在(0,1)上为增函数, h(x)max<2……………………………8分
h(x)max<2……………………………8分

 ……………………………………………………………………9分
……………………………………………………………………9分
(Ⅲ)设 则
则 =
= ……10分
……10分
即 ,对
,对 恒成立…………………………11分
恒成立…………………………11分

 ,对
,对 恒成立
恒成立
即 对
对 恒成立…………………………13分
恒成立…………………………13分


解得 ……………………………………………………14分
……………………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com