
题目列表(包括答案和解析)
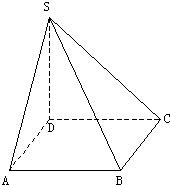 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=| 3 |
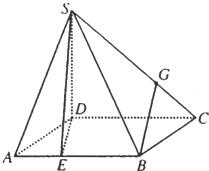 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=3
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=3| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
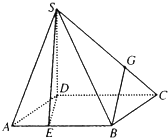 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=3
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=3| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
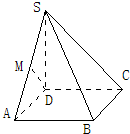 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=| 3 |
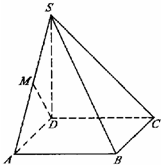 如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=| 3 |
一.选择题:CBDCC BDBDA
解析:1: 由文氏图可得结论(C).
2:由已知得:( -2
-2 )
)
 =0,(
=0,( -2
-2 )
)
 =0;即得:
=0;即得: =
= =2
=2

 ,∴cos<
,∴cos< ,
, >=
>= ,∴选(B)
,∴选(B)
3:由于受条件sin2θ+cos2θ=1的制约,故m为一确定的值,于是sinθ,cosθ的值应与m的值无关,进而推知tan 的值与m无关,又
的值与m无关,又 <θ<π,
<θ<π, <
< <
< ,∴tan
,∴tan >1,故选D。
>1,故选D。
4:由于 ,从而函数
,从而函数 的一个背景为正切函数tanx,取
的一个背景为正切函数tanx,取 ,可得必有一周期为4
,可得必有一周期为4 。故选C。
。故选C。
5:解此题具有很大的迷惑性,注意题目隐含直线AB的方程就是 ,它过定点(0,2),只有C项满足。故选C。
,它过定点(0,2),只有C项满足。故选C。
6:生活常识告诉我们利息税的税率是20%。故选B。
7:四个选项中只有答案D含有分数,这是何故?宜引起高度警觉,事实上,将x值取4.5代入验证,不等式成立,这说明正确选项正是D,而无需繁琐地解不等式。
8:(用排除法)七人并排站成一行,总的排法有 种,其中甲、乙两人相邻的排法有2×
种,其中甲、乙两人相邻的排法有2× 种.因此,甲、乙两人必需不相邻的排法种数有:
种.因此,甲、乙两人必需不相邻的排法种数有: -2×
-2× =3600,对照后应选B;
=3600,对照后应选B;
 9:作直线
9:作直线 的图象和半圆
的图象和半圆 ,从图中可以看出:
,从图中可以看出:  的取值范围应选(D).
的取值范围应选(D).
注:求与方程实数根个数有关的问题常用图解法.
 10:如图,将正四面体ABCD补形成正方体,则正四面体、正方体的中心与其外接球的球心共一点.因为正四面体棱长为
10:如图,将正四面体ABCD补形成正方体,则正四面体、正方体的中心与其外接球的球心共一点.因为正四面体棱长为 ,所以正方体棱长为1,从而外接球半径R=
,所以正方体棱长为1,从而外接球半径R= .故S球=3
.故S球=3 .
.
二.填空题:11、 ; 12、
; 12、 ; 13、
; 13、 或
或 或
或 ;
;
14、+1; 15、3;
解析:11: ,由复合函数的增减性可知,
,由复合函数的增减性可知, 在
在 上为增函数,∴
上为增函数,∴ ,∴
,∴ 。
。
12:计算机进行运算: 时,它表示的表达式是
时,它表示的表达式是 ,当其有意义时,得
,当其有意义时,得 ,解得
,解得 .
.
13: 本题是一道很好的开放题,解题的开窍点是:每个面的三条棱是怎样构造的,依据“三角形中两边之和大于第三边”,就可否定{1,1,2},从而得出{1,1,1},{1,2,2},{2,2,2}三种形态,再由这三类面构造满足题设条件的四面体,最后计算出这三个四面体的体积分别为:
 ,
, ,
, ,故应填.
,故应填. 、
、 、
、 中的一个即可.
中的一个即可.
14.解:直线: 化为一般方程:
化为一般方程: ,点P
,点P 化为点
化为点 ,则点
,则点 到直线的距离为
到直线的距离为
15解:由△COF∽△PDF得 ,即
,即 =
=
= =
= ,即
,即 =
= ,
,
解得 ,故
,故 =3
=3
三.解答题:
16.解:当P为真时,有 ……4分
……4分
当Q为真时,有 ……5分
……5分
 ……6分
……6分
由题意:“P或Q”真,“P且Q”为假 等价于
(1)P真Q假: ……8分
……8分
(2)Q真P假: ……11分
……11分
综合(1)(2) 的取值范围是
的取值范围是 ……12分
……12分
17.解:(1)∵ ∴
∴
∵ ∴
∴ ,
,  即AB边的长度为
即AB边的长度为 ……………………3分
……………………3分
(2) 由 得
得 -------------①
-------------①
 即
即 -------------②
-------------②
由①②得 , 由正弦定理得
, 由正弦定理得
∴ ∴
∴ -- ……………………8分
-- ……………………8分
(3) ∵ ,由(2)中①得
,由(2)中①得 由余弦定理得
由余弦定理得 =
=
∴ =
= - ……………………12分
- ……………………12分
18.解:(Ⅰ) ,
, , ……………1分
, ……………1分
由题意,知 ,
,
 ,
,
即 ……………………2分
……………………2分
 …………………3分
…………………3分
①
当 时,
时, ,函数
,函数 在区间
在区间 上单调增加,
上单调增加,
不存在单调减区间; ……………………5分
②
当 时,
时, ,有
,有





+
-
+




 当
当 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为 ……………7分
……………7分
③
当 时,
时,  ,有
,有





+
-
+




 当
当 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为 …………9分
…………9分
(Ⅱ)由(Ⅰ)知:若 不是函数
不是函数 的极值点,则
的极值点,则 ,
,

 …………………10分
…………………10分
设点 是函数
是函数 的图像上任意一点,则
的图像上任意一点,则 ,
,
点 关于点
关于点 的对称点为
的对称点为 ,
,

(或  )
)
 点
点 在函数
在函数 的图像上.
的图像上.
 由点
由点 的任意性知函数
的任意性知函数 的图像关于点
的图像关于点 对称.
…………………14分
对称.
…………………14分
19. [方法一]:(几何法)
(I)证法一:如图1,∵底面ABCD是正方形, ∴BC⊥DC.
∵SD⊥底面ABCD,∴DC是SC在平面ABCD上的射影,
由三垂线定理得BC⊥SC. …………3分
证法二:如图1,∵底面ABCD是正方形, ∴BC⊥DC.
∵SD⊥底面ABCD,∴SD⊥BC,又DC∩SD=D, 图1
∴BC⊥平面SDC,∴BC⊥SC. …………3分
(II)解法一:∵SD⊥底面ABCD,且ABCD为正方形,
 ∴可把四棱锥S―ABCD补形为长方体A1B1C1S―ABCD,
∴可把四棱锥S―ABCD补形为长方体A1B1C1S―ABCD,
如图2,面ASD与面BSC所成的二面角就是面ADSA1与面BCSA1所成的二面角,
∵SC⊥BC,BC//A1S, ∴SC⊥A1S,
又SD⊥A1S,∴∠CSD为所求二面角的平面角.
在Rt△SCB中,由勾股定理得SC= ,在Rt△SDC中,
,在Rt△SDC中,
由勾股定理得SD=1.
∴∠CSD=45°.即面ASD与面BSC所成的二面角为45°. ……………8分
解法二:如图3,过点S作直线
 在面ASD上,
在面ASD上,
∵底面ABCD为正方形, 在面BSC上,
在面BSC上,

∴∠CSD为面ASD与面BSC所成二面角的平面角.
在Rt△SCB中,由勾股定理得SC= ,在Rt△SDC中,
,在Rt△SDC中,
由勾股定理得SD=1.
∴∠CSD=45°.即面ASD与面BSC所成的二面角
为 45°。…8分
(III)解法一:如图3, ∵SD=AD=1,∠SDA=90°, ∴△SDA是等腰直角三角形.
又M是斜边SA的中点, ∴DM⊥SA.
∵BA⊥AD,BA⊥SD,AD∩SD=D,∴BA⊥面ASD,SA是SB在面ASD上的射影.
由三垂线定理得DM⊥SB. ∴异面直线DM与SB所成的角为90°. ……………14分
在△ABS中,由中位线定理得 MP//SB, 是异面直线DM与SB所成的角.
是异面直线DM与SB所成的角.
 ,
,
又
∴在△DMP中,有DP2=MP2+DM2, 
即异面直线DM与SB所成的角为90°. ……………14分
解析:如图所示,以D为坐标原点建立直角坐标系,
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),
M( ,0,
,0, ),
),
∵ SB= ,DB=
,DB= ,SD=1,∴ S(0,0,1),……………2分
,SD=1,∴ S(0,0,1),……………2分
(I)证明:∵  ,
,

 =0 ∴
=0 ∴  ,即BC
,即BC SC.……………5分
SC.……………5分
(II)设二面角的平面角为θ,由题意可知平面ASD的一个法向量为 ,设平面BSC的法向量为
,设平面BSC的法向量为 ,由
,由


 ,
,
得
 ,
,
∴ 面ASD与面BSC所成的二面角为45°.……………10分
(III)设异面直线DM与SB所成角为α,
 ∵
∵  ,SB=(-1,-1,1),得
,SB=(-1,-1,1),得

∴ 异面直线DM与SB所成角为90°.……………14分

20.解:(1)设圆心 的坐标为
的坐标为 ,如图过圆心
,如图过圆心 作
作 轴于H,
轴于H,
则H为RG的中点,在 中,
中, …3分
…3分
∵ ∴
∴
即 …………………6分
…………………6分
(2) 设 ,
,
直线AB的方程为 (
( )则
)则 -----①
-----① ---②
---②
∵点 在直线
在直线 上, ∴
上, ∴ .
.
∴点M的坐标为 . ………………10分
. ………………10分
同理可得: ,
,  ,
,
∴点 的坐标为
的坐标为 . ………………11分
. ………………11分
直线 的斜率为
的斜率为 ,其方程为
,其方程为
 ,整理得
,整理得 ,………………13分
,………………13分
显然,不论 为何值,点
为何值,点 均满足方程,
均满足方程,
∴直线 恒过定点
恒过定点 .……………………14分
.……………………14分
21.解:(Ⅰ)当n=1时,D1为Rt△OAB1的内部包括斜边,这时
 ,
,
当n=2时,D2为Rt△OAB2的内部包括斜边,这时
 ,
,
当n=3时,D3为Rt△OAB3的内部包括斜边,这时
 ,……, ---3分
,……, ---3分
 由此可猜想
由此可猜想 =3n。
--------------------------------------------------4分
=3n。
--------------------------------------------------4分
下面用数学归纳法证明:
(1) 当n=1时,猜想显然成立。
(2) 假设当n=k时,猜想成立,即 ,(
,( ) ----5分
) ----5分
如图,平面区域 为Rt
为Rt 内部包括斜边、平面区域
内部包括斜边、平面区域 为
为
Rt△ 内部包括斜边,∵平面区域
内部包括斜边,∵平面区域 比平面区域
比平面区域 多3
多3
个整点, ------- 7分
即当n=k+1时, ,这就是说当n=k+1时,
,这就是说当n=k+1时,
猜想也成立,
由(1)、(2)知 =3n对一切
=3n对一切 都成立。 ---------------------8分
都成立。 ---------------------8分
(Ⅱ)∵ =3n, ∴数列
=3n, ∴数列 是首项为3,公差为3的等差数列,
是首项为3,公差为3的等差数列,
∴ .
.
 -------------------------10分
-------------------------10分


= =
= -------------------------------11分
-------------------------------11分
∵对一切 ,
, 恒成立, ∴
恒成立, ∴
∵ 在
在 上为增函数 ∴
上为增函数 ∴ ---13分
---13分
 ,满足
,满足 的自然数为0,
的自然数为0,
∴满足题设的自然数m存在,其值为0。 -------------------------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com