
题目列表(包括答案和解析)
(12分)设△![]() 三边长为
三边长为![]() ,与之对应的三条高分别为
,与之对应的三条高分别为![]() ,若满足关系:
,若满足关系:![]()
(Ⅰ)求证:![]() 是△
是△![]() 的面积);
的面积);
围建一个面积为360 m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2 m的进出口,如图所示已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)

(1)将y表示为x的函数;
(2)写出f(x)的单调区间,并证明;
(3)根据(2),试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
已知椭圆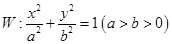 的焦距为
的焦距为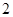 ,过右焦点和短轴一个端点的直线的斜率为
,过右焦点和短轴一个端点的直线的斜率为 ,
,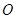 为坐标原点.
为坐标原点.
(1)求椭圆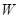 的方程.
的方程.
(2)设斜率为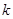 的直线
的直线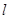 与
与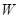 相交于
相交于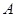 、
、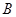 两点,记
两点,记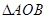 面积的最大值为
面积的最大值为 ,证明:
,证明: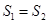 .
.
 的焦距为
的焦距为 ,过右焦点和短轴一个端点的直线的斜率为
,过右焦点和短轴一个端点的直线的斜率为 ,
, 为坐标原点.
为坐标原点. 的方程.
的方程. 的直线
的直线 与
与 相交于
相交于 、
、 两点,记
两点,记 面积的最大值为
面积的最大值为 ,证明:
,证明: .
.设函数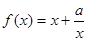 定义域为
定义域为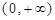 ,且
,且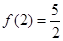 .设点
.设点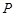 是函数图像上的任意一点,过点
是函数图像上的任意一点,过点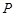 分别作直线
分别作直线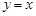 和
和
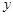 轴的垂线,垂足分别为
轴的垂线,垂足分别为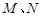 .
.

(1)写出 的单调递减区间(不必证明);
的单调递减区间(不必证明);
(2)问: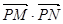 是否为定值?若是,则求出该定值,若不是,则说明理由;
是否为定值?若是,则求出该定值,若不是,则说明理由;
(3)设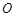 为坐标原点,求四边形
为坐标原点,求四边形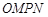 面积的最小值.
面积的最小值.
一.选择题:AACBD DCDAD
解析:1:可以判定对应法则 是从A到C的函数(
是从A到C的函数( ,且
,且 是该函数的值域),于是对于实数
是该函数的值域),于是对于实数 ,在集合A中不存在原象,则
,在集合A中不存在原象,则 的取值范围构成集合
的取值范围构成集合 ,注意到
,注意到 ,故
,故 ,
, .
.
从而答案为A.
2: 前三年年产量的增长速度越来越快,总产量C与时间t(年)的函数关系,在图上反映出来,当 时是选项A、C中的形状;又后三年年产量保持不变,总产量C与时间t(年)的函数关系应如选项A所示,于是选A.
时是选项A、C中的形状;又后三年年产量保持不变,总产量C与时间t(年)的函数关系应如选项A所示,于是选A.
3: 利用图象法求之.其中F(x)=  于是选C
于是选C
4:由题意得 ,
,  于是
于是
 于是选B
于是选B
5:⑴静放在点 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点 沿直线出发,经椭圆壁右顶点反弹后第一次回到点
沿直线出发,经椭圆壁右顶点反弹后第一次回到点 时,小球经过的路程是
时,小球经过的路程是 ,则选B;
,则选B;
⑵静放在点 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点 沿直线出发,经椭圆壁左顶点反弹后第一次回到点
沿直线出发,经椭圆壁左顶点反弹后第一次回到点 时,小球经过的路程是
时,小球经过的路程是 ,则选C;
,则选C;
⑶静放在点 的小球(小球的半径不计)从点
的小球(小球的半径不计)从点 沿直线出发,经椭圆壁非左右顶点反弹后第一次回到点
沿直线出发,经椭圆壁非左右顶点反弹后第一次回到点 时,小球经过的路程是
时,小球经过的路程是 ,则选A。
,则选A。
于是三种情况均有可能,故选D。
6:用条件代入计算,不难得到结论为D.
7:解法一 因ysinx+cosx=2,故 .
.
由 ,得
,得  ,于是
,于是 . 因0<x<π,故y>0.又当
. 因0<x<π,故y>0.又当 时,
时, .若x=
.若x= ,有
,有 ,故ymin=
,故ymin= ,选C.
,选C.
解法二 由已知得:ysinx = 2 - cosx,于是y2(1-cos2x) = (2-cosx)2.
将上式整理得:(y2+1)cos2x-4cosx+4-y2=0.于是,ㄓ=16-4(y2+1)(4-y2)=4y2(y2-3)≥0.
因0<x<π,故y>0,于是y≥ ,而当y=
,而当y= 时,ㄓ=0,cosx=
时,ㄓ=0,cosx= ,x=
,x= 满足题设,于是ymin=
满足题设,于是ymin= ,选C.
,选C.
 解法三 设
解法三 设 ,则
,则

 ,当且仅当
,当且仅当
 ,即
,即
 ,亦即x=
,亦即x= 时,取“=”,故ymin=
时,取“=”,故ymin= ,选C.
,选C.
解法四 如图,单位圆中,∠MOt = ,P(2,0),M(cosx,sinx),
,P(2,0),M(cosx,sinx), .
.
因 ,故∠AOP=
,故∠AOP= ,∠APt =
,∠APt = ,
,
 ,从而,(kPM)min=
,从而,(kPM)min= .
.
8:由于函数 的图像关于原点中心对称,则
的图像关于原点中心对称,则
为奇函数,于是 ,
, ,从而
,从而 ,
, ,当
,当 ,验正之选D.
,验正之选D.
9:集合A的子集为 共8个,
共8个,
集合A的一个分拆可以列表如下:
A1




A2





A1




A2
 ,
, 


 ,
, ,
,


 ,
,

 ,
, ,
, ,
, ,
,

 ,
,
共有27个,选A.
 10:从10个不同的点中任取4个点的不同取法共有
10:从10个不同的点中任取4个点的不同取法共有 =210种,它可分为两类:4点共面与不共面.
=210种,它可分为两类:4点共面与不共面.
如图1,4点共面的情形有三种:
①取出的4点在四面体的一个面内(如图中的AHGC在面ACD内),这样的取法有 种;
种;
②取出的4面所在的平面与四面体的一组对棱平行(如图中的EFGH与AC、BD平行),这种取法有3种(因为对棱共3组,即AC与BD、BC与AD、AB与CD);
③取出的4点是一条棱上的三点及对棱中点(如图中的AEBG),这样的取法共6种.
综上所述,取出4个不共面的点的不同取法的种数为 -(
-( +3+6)=141种.
+3+6)=141种.
故所求的概率为 ,答案选D.
,答案选D.
二.填空题:11、91万元; 12、 ; 13、②⑦④; ②④⑦; ④②⑦;
⑤②④; ⑤④②;
④⑤②. 14、:y2=x; 15、
; 13、②⑦④; ②④⑦; ④②⑦;
⑤②④; ⑤④②;
④⑤②. 14、:y2=x; 15、 ;
;
解析:
11:不少于1万元的占700万元的21%, 为700×21%=147万元.
1万元以上的保单中,超过或等于2.5万元的保单占 ,
,
金额为 ×147=91万元,故不少于2.5万元的保险单有91万元。
×147=91万元,故不少于2.5万元的保险单有91万元。
12:原不等式可化为:(1) ,即
,即 ;
;
(2) 解得
解得 ;(3)
;(3) 即
即 , 综上得:
, 综上得:
13:根据三角函数的图像的变换情况,不难得出下列6种变换:
②⑦④; ②④⑦; ④②⑦; ⑤②④; ⑤④②; ④⑤②.
14:依题意有  ,即
,即 ,消去参数
,消去参数 ,可得:y2=x
,可得:y2=x
15:连结AD、DE,则AD=DE,
 ,又
,又 ,
,
 ,
, ,即
,即 =
= ,即
,即 ,
,

三.解答题:
16.解:(1) ………………2分
………………2分

 ……………………………………6分
……………………………………6分
(2)

①当 时,当县仅当
时,当县仅当 时,
时, 取得最小值-1,这与已知矛盾;…8分
取得最小值-1,这与已知矛盾;…8分
②当 时,
时, 取得最小值
取得最小值 ,由已知得
,由已知得
 ;……………………………………………………………10分
;……………………………………………………………10分
③当 时,
时, 取得最小值
取得最小值 ,由已知得
,由已知得
解得 ,这与
,这与 相矛盾,综上所述,
相矛盾,综上所述, 为所求。……………………12分
为所求。……………………12分
17、解:(1)记“抛掷1枚硬币1次出现正面向上”为事件A,P(A)= ,抛掷15枚硬币1次相当于作15次独立重复试验,根据
,抛掷15枚硬币1次相当于作15次独立重复试验,根据 次独立重复试验中事件A发生K次的概率公式,记至多有一枚正面向上的概率为P1
次独立重复试验中事件A发生K次的概率公式,记至多有一枚正面向上的概率为P1
则P1=
P15(0)+ P15(1)= +
+ =
= ……………6分
……………6分
(2)记正面向上为奇数枚的概率为P2,则有
P2= P15(1)+
P15(3)+…+
P15(15)= +
+ +…+
+…+
= +…+
+…+ )?
)? ………………………10分
………………………10分
又“出现正面向上为奇数枚”的事件与“出现正面向上为偶数枚”的事件是对立事件,记“出现正面向上为偶数枚”的事件的概率为P3
 P3=1?
P3=1? =
=
 出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率相等 ………12分
出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率相等 ………12分
18、解:(Ⅰ)
 ;
……2分
;
……2分
(Ⅱ)性质①、②均可推广,推广的形式分别是:
① ,
②
,
② ……4分
……4分
事实上,在①中,当 时,左边
时,左边 , 右边
, 右边 ,等式成立;
,等式成立;
当 时,左边
时,左边

 , 因此,①
, 因此,① 成立;
……6分
成立;
……6分
在②中,当 时,左边
时,左边 右边,等式成立;
右边,等式成立;
当 时,
时,
左边



 右边,
右边,
因此 ② 成立。 ……8分
成立。 ……8分
(Ⅲ)先求导数,得 .
.
令 >0,解得x<
>0,解得x< 或 x>
或 x> .
.
因此,当 时,函数为增函数, ……11分
时,函数为增函数, ……11分
当 时,函数也为增函数。
时,函数也为增函数。
令 <0,解得
<0,解得 <x<
<x< .
.
因此,当 时,函数为减函数. ……13分
时,函数为减函数. ……13分
所以,函数 的增区间为
的增区间为 ,
, 
 函数
函数 的减区间为
的减区间为 ……14分
……14分
19、解:(Ⅰ)如图所示:
C(2,0,0),S(0,0,1),O(0,0,0),B(1,1,0)

………………………………………………………5分
(Ⅱ)①

……………………………………………………………………………8分
② ,
,

 ,
,


③
 ;
; ……………………………………14分
……………………………………14分
20、解:(1)依题意,⊙ 的半径
的半径 ,
,
 ⊙
⊙ 与⊙
与⊙ 彼此外切,
彼此外切,
 …………………………………2分
…………………………………2分 
两边平方,化简得  ,
,
即  ,
…………………………………4分
,
…………………………………4分
 ,
, 

 , ∴ 数列
, ∴ 数列 是等差数列. …………………7分
是等差数列. …………………7分
(2)
由题设, ,∴
,∴ ,即
,即 ,
,
 ,
,

 …………………………………9分
…………………………………9分 

= ………………12分
………………12分
=
 . …………………………………14分
. …………………………………14分
21:(Ⅰ)证明:由题意设
由 得
得 ,则
,则 所以
所以
因此直线MA的方程为
直线MB的方程为 …………………2分
…………………2分
所以 ①
①  ②
②
由①、②得  因此
因此  ,即
,即
所以A、M、B三点的横坐标成等差数列. …………………4分
(Ⅱ)解:由(Ⅰ)知,当x0=2时, 将其代入①、②并整理得:

 所以 x1、x2是方程
所以 x1、x2是方程 的两根,
的两根,
因此 又
又
所以 …………………6分
…………………6分
由弦长公式得 
又 , 所以p=1或p=2,
, 所以p=1或p=2,
因此所求抛物线方程为 或
或 …………………8分
…………………8分
(Ⅲ)解:设D(x3,y3),由题意得C(x1+ x2, y1+ y2),
则CD的中点坐标为
设直线AB的方程为
由点Q在直线AB上,并注意到点 也在直线AB上,
也在直线AB上,
代入得
若D(x3,y3)在抛物线上,则
因此 x3=0或x3=2x0.
即D(0,0)或 …………………10分
…………………10分
(1)当x0=0时,则 ,此时,点M(0,-2p)适合题意. ………………11分
,此时,点M(0,-2p)适合题意. ………………11分
(2)当 ,对于D(0,0),此时
,对于D(0,0),此时
又 AB⊥CD,
所以
AB⊥CD,
所以 ………………12分
………………12分
即 矛盾.
矛盾.
对于 因为
因为 此时直线CD平行于y轴,
此时直线CD平行于y轴,
又
所以 直线AB与直线CD不垂直,与题设矛盾,
所以 时,不存在符合题意的M点.
时,不存在符合题意的M点.
综上所述,仅存在一点M(0,-2p)适合题意. ………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com