题目列表(包括答案和解析)
（04年天津卷）（12分）
已知
(I)求
的值；
(II)求
的值。
设
的内角A、B、C所对的边分别为a、b、c，已知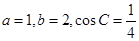
(I)求的第三条边长c；
(II)求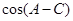
的值。
本题有（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）（本小题满分7分）选修4-2：矩阵与变换
已知矩阵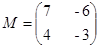
，向量
．
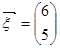(I)求矩阵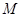
的特征值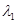
、
和特征向量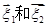
；
(II)求
的值．
（2）（本小题满分7分）选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知曲线C的参数方程为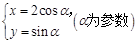
．以直角坐标系原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为
．
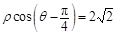（Ⅰ）求直线l的直角坐标方程；
（Ⅱ）点P为曲线C上的动点，求点P到直线l距离的最大值．
（3）（本小题满分7分）选修4-5：不等式选讲
（Ⅰ）已知：a、b、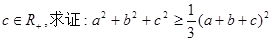
；www.7caiedu.cn
（Ⅱ）某长方体从一个顶点出发的三条棱长之和等于3，求其对角线长的最小值.
本题有（1）、（2）、（3）三个选答题，每小题7分，请考生任选2题作答，满分14分，如果多做，则按所做的前两题计分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．
（1）（本小题满分7分）选修4-2：矩阵与变换
已知矩阵
，向量
．
(I)求矩阵
的特征值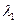
、
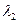和特征向量
；
(II)求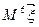
的值．
（2）（本小题满分7分）选修4-4：坐标系与参数方程
在平面直角坐标系xOy中，已知曲线C的参数方程为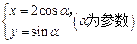
．以直角坐标系原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为
．
（Ⅰ）求直线l的直角坐标方程；
（Ⅱ）点P为曲线C上的动点，求点P到直线l距离的最大值．
（3）（本小题满分7分）选修4-5：不等式选讲
（Ⅰ）已知：a、b、
；w.w.w.k.s.5.u.c.o.m
（Ⅱ）某长方体从一个顶点出发的三条棱长之和等于3，求其对角线长的最小值.
（本小题满分12分）
已知
(I)求
的值；
(II)求
的值。
一、选择题：本大题共10小题，每小题5分，共50分.
CABCA，BCDDC
二、填空题：本大题共5小题，每小题5分 ，共25分，
11. 12； 12. 
； 13. 8； 14. x－2y－z+3=0； 15. ②④.
三、解答题：本大题共6小题，共75分. 解答应写出文字说明，证明过程或演算步骤.
16.解：(Ⅰ)
由已知 
， ∴ 
，
又 ΔABC是锐角三角形， ∴ 
………………………………6分
(Ⅱ) 
………………………………12分
17.解法一：（Ⅰ）∵
，
且 
∴ 
， ……………………3分
∵ 
∴ 
……………………6分
（Ⅱ）取
的中点
，则
，连结
，
∵
，∴
，从而
作
，交
的延长线于
，连结
，则由三垂线定理知， AC⊥MH，
从而
为二面角
的平面角
…………………8分
直线
与直线
所成的角为
，∴
…………………9分
在
中，由余弦定理得
在
中，
在
中，
在
中，
故二面角
的平面角大小为
…………………12分
解法二：（Ⅰ）同解法一
（Ⅱ）在平面
内，过
作
，建立空间直角坐标系
（如图）
由题意有
，设
，
则
………5分
由直线
与直线
所成的角为
，得
，即
，解得
………7分
∴
，设平面
的一个法向量为
，
则
，取
，得
……………9分
又 平面的法向量取为
……………10分
设
与
所成的角为
，则
，
故二面角的平面角大小为
……………12分
18. 解：(I)记“幸运观众获得奖金5000元”为事件M，即前两个问题选择回答A、C且答对，最后在回答问题B时答错了.
故 幸运观众获得奖金5000元的概率为 
………………6分
(II) 设幸运观众按A→B→C顺序回答问题所得奖金数为随机变量ξ，则ξ的取值可以为0元、1000元、3000元和7000元，其分布列为
0
1000
3000
7000
P
∴ 
元. ………………9分
设幸运观众按C→B→A顺序回答问题所得奖金数为随机变量η，则η的取值可以为0元、4000元、6000元和7000元，其分布列为
η
0
4000
6000
7000
P
∴ 
元. ……11分
故 乙观众的选择所获奖金期望较大. ………………12分
19.解：（1）∵ 
……………………2分
由已知
对
恒成立，即
对恒成立
又 
∴ 
为所求 …………………………5分
（2）取
， ∵ 
， ∴ 
由已知
在
上是增函数，即
，
也就是
即 
…………8分
另一方面，设函数
，则 
∴
在
上是增函数，又
∴
当
时，
∴
，即 
综上所述，
………………………………………………13分
20.解：(Ⅰ) 由题意可知，平面区域
如图阴影所示． …3分
设动点为
，则
，即
．
由 
知
，x－y<0，即x2－y2<0．
所以 y2－x2＝4(y>0)，即为曲线的方程 …………6分
(Ⅱ)设
，
，则以线段
为直径的圆的圆心为
.
因为以线段为直径的圆
与
轴相切，所以半径 
，
即 
………………………8分
因为直线AB过点
，当AB ^ x轴时，不合题意．
所以设直线AB的方程为 y＝k(x－2)．
代入双曲线方程y2－x2＝4 (y＞0)得: (k2－1)x2－4k2x＋(8k2－4)＝0．
因为直线l与双曲线交于A，B两点，所以k≠±1．于是
x1＋x2＝，x1x2＝．
∴ |AB|=
∴ 
化简得：k4＋2k2－1＝0 ……………………………11分
解得: k2＝－1 （k2＝－－1不合题意，舍去）．
由△＝(4k2)2－4(k2－1)(8k2－4)＝3k2－1＞0，又由于y＞0，所以－1<k<－ ．
所以直线l存在,其斜率为 k＝－. …………………13分
21. 解：(1) 因为 
,所以
,
于是: 
, 即
是以2为公比的等比数列.
|
，解得：
,
且
，所以
，于是
. ……3分
得：
是正整数列, 所以 
.
, 所以 
，…………………5分
得：
. 
得：
…………………6分
①
②
时，①式减去②式, 得
的前
项和 
．……………8分
时，
．这时数列
项和
．…………9分
的第一项
最大，下面证明：
③
知
，要使③式成立，只要 
，
，使得
对任意
均成立． ……………13分以!