（2012•湖北模拟）某校高二年级共有学生1000名，其中走读生750名，住宿生250名，现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查，根据问卷取得了这n名同学每天晚上有效学习时间（单位：分钟）的数据，按照以下区间分为八组：[0，30），[30，60），[60，90），[90，120），[120，150），[150，180），[180，210），[210.240），得到频率分布直方图如图，已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人．
（1）求n的值并求有效学习时间在[90，120）内的频率；
（2）如果把“学生晚上有效时间达到两小时”作为是否充分利用时间的标准，对抽取的n名学生，下列2×2列联表，问：是否有95%的把握认为学生利用时间是否充分与走读、住宿有关？

	利用时间充分	利用时间不充分	合计
走读生	50	a	75 75
住校生	b	15	25 25
合计	60 60	40	n

（3）若在第①组、第②组、第⑦组、第⑧组中共抽出3人调查影响有效利用时间的原因，记抽到“有效学习时间少于60分钟”的学生人数为X，求X的分布列及期望．
参考公式：K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

参考列表：

P（K2≥k0）	0.50	0.40	0.25	0.15	0.10	0.05	0.025
k0	0.455	0.708	1.323	2.072	2.706	3.841	5.024

（2013•韶关二模）以下四个命题
①在一次试卷分析中，从每个试室中抽取第5号考生的成绩进行统计，是简单随机抽样；
②样本数据：3，4，5，6，7的方差为2；
③对于相关系数r，|r|越接近1，则线性相关程度越强；
④通过随机询问110名性别不同的行人，对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查，得到如下列联表：

	男	女	总计
走天桥	40	20	60
走斑马线	20	30	50
总计	60	50	110

附表：

P（K2≥k）	0.05	0.010	0.001
k	3.841	6.635	10.828

由K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

可得，k²=

110×(40×30-20×20)

60×50×60×50

=7.8，
则有99%以上的把握认为“选择过马路方式与性别有关”．其中正确的命题序号是．

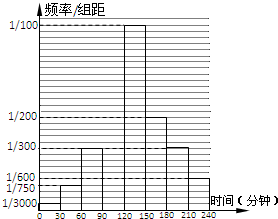某校高二年级共有学生1000名，其中走读生750名，住宿生250名，现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查．根据问卷取得了这n名同学每天晚上有效学习时间（单位：分钟）的数据，按照以下区间分为八组：
①[0，30），②[30，60），③[60，90），④[90，120），
⑤[120，150），⑥[150，180），⑦[180，210），⑧[210，240），
得到频率分布直方图如下．已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人；
（1）求n的值并补全下列频率分布直方图；
（2）如果把“学生晚上有效时间达到两小时”作为是否充分利用时间的标准，对抽取的n名学生，完成下列2×2列联表：

	利用时间充分	利用时间不充分	总计
走读生	50	25	75
住宿生	10	15	25
总计	60	40	100

是否有95%的把握认为学生利用时间是否充分与走读、住宿有关？
参考公式：K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

参考列表：

P（K2≥k0）	0.50	0.40	0.25	0.15	0.10	0.05	0.025
k0	0.455	0.708	1.323	2.072	2.706	3.841	5.024

（3）若在第①组、第②组、第⑦组、第⑧组中共抽出3人调查影响有效利用时间的原因，记抽到“有效学习时间少于60分钟”的学生人数为X，求X的分布列及期望．