题目列表(包括答案和解析)
C．选修4-4：坐标系与参数方程
在极坐标系下，已知圆O：
和直线
，
（1）求圆O和直线
的直角坐标方程；（2）当
时，求直线与圆O公共点的一个极坐标.
D．选修4-5：不等式证明选讲
对于任意实数
和
，不等式
恒成立，试求实数
的取值范围．
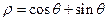和直线
，
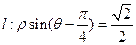的直角坐标方程；（2）当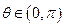
时，求直线与圆O公共点的一个极坐标.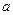
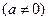和
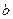，不等式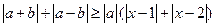
恒成立，试求实数
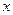的取值范围．| x2 |
| m-2 |
| y2 |
| 6-m |
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
C
[解析] 由基本不等式，得ab≤
＝
＝
－ab，所以ab≤
，故B错；
＋
＝
＝
≥4，故A错；由基本不等式得
≤
＝
，即
＋
≤
，故C正确；a2＋b2＝(a＋b)2－2ab＝1－2ab≥1－2×＝，故D错．故选C.
一、 选择题（每小题5分，共50分.请把正确选择支号填在答题表内.）
1―5 DADBA 6―10 BADCB
二、填空题（每小题5分，共20分）：
11.84； 12.e-2； 13.8； 14.3；
三、解答题：本大题共6小题，共80分. 解答应写出文字说明、证明过程或演算步骤.
15（本小题满分12分）
解（1）∵
//
，
①若，共向，则 
＝||•||＝
………………… 3′
②若，异向，则 ＝－||•||＝－ ……………… 6′
（2）∵，的夹角为135°， ∴ ＝||•||•cos135°＝－1 …… 8′
∴|＋|2＝（＋）2 ＝2＋2＋2＝1＋2－2＝1 ………… 11′
∴
……………………………………12
16. （本小题满分13分）
解：（1）函数可化简为f ( x
) = cos
，
3分
最小正周期为
；
4分
当
时，f ( x
)取得最大值1
5分
取得最大值时x的取值集合为
6分
（2）由
得对称轴方程为：
，其中
9分
（3）由于f ( x
) = cos，
把f ( x )图像上各点向左平移
个单位，得到 y=cos2x
11分
再把所得图像上各点的横线坐标缩短到原来的2倍，纵坐标不变,得到y=cosx
13分
17. （本小题满分13分）
解：（1）由已知得
解得
．…………………1分
设数列
的公比为
，由，可得
．
又
，可知
，即
， ……………3分
解得
．
由题意得
． 
．………………………………………………
5分
故数列的通项为
． …
………………………………7分
（2）由于
由（1）得
…………………………9分
又
是等差数列．
…………………………………………11分
…………………13分
18（本小题满分13分）
解：如图，连结
，由已知
，。。。。。。。1分
， 。。。。。。。。。。2分
，
又
，。。。。。3分
是等边三角形， 。。。。。4分
，
由已知，
，
，。。。。。。。。。6分
在
中，由余弦定理，
．
。。。。。。。。。。。。。10分
． 。。。。。。。。。。11分
因此，乙船的速度的大小为
（海里/小时）．。。。。。。12分
答：乙船每小时航行
海里． 。。。。。。。。。。。。。。。。。。。。。。。。13分
29．（本小题满分14分）
解:(1)
20. （本小题满分15分）
解：（1）
时，f（x）＞1
令x=－1，y=0则f（－1）=f（－1）f（0）∵f（－1）＞1
∴f（0）=1……………………………3′
若x＞0，则f（x－x）=f（0）=f（x）f（－x）故
故x∈R f（x）＞0…………………………………………………5分
任取x1＜x2 
故f（x）在R上减函数………………………………………..7分
（2）①
由f（x）单调性
…9分
得：an+1=an+2 故{an}等差数列 
………………………10分
②
是递增数列………………12分
当n≥2时，
……………………………13分
即
而a＞1，∴x＞1
故x的取值范围（1，+∞）……………………………15分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com