
题目列表(包括答案和解析)
在数列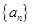 中,
中,
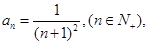 记
记
(Ⅰ)求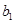 、
、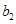 、
、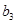 、
、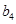 并推测
并推测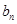 ;
;
(Ⅱ)用数学归纳法证明你的结论.
【解析】第一问利用递推关系可知,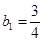 、
、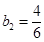 、
、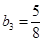 、
、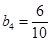 ,猜想可得
,猜想可得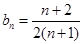
第二问中,①当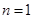 时,
时,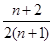 =
=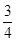 ,又
,又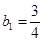 ,猜想正确
,猜想正确
②假设当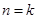 时猜想成立,即
时猜想成立,即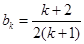 ,
,
当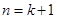 时,
时,
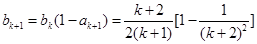 =
=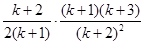
=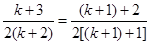 ,即当
,即当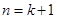 时猜想也成立
时猜想也成立
两步骤得到。
(2)①当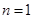 时,
时,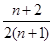 =
=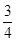 ,又
,又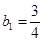 ,猜想正确
,猜想正确
②假设当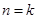 时猜想成立,即
时猜想成立,即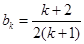 ,
,
当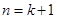 时,
时,
 =
=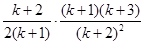
=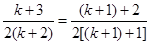 ,即当
,即当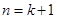 时猜想也成立
时猜想也成立
由①②可知,对于任何正整数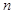 都有
都有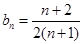 成立
成立
已知点 为圆
为圆 上的动点,且
上的动点,且 不在
不在 轴上,
轴上, 轴,垂足为
轴,垂足为 ,线段
,线段 中点
中点 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点
 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线 交于
交于 、
、 两点。
两点。
(I)求曲线 的方程;
的方程;
(II)试证明:在 轴上存在定点
轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
【解析】第一问中设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为
第二问中,设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得 
∵ ,∴
,∴
确定结论直线 与曲线
与曲线 总有两个公共点.
总有两个公共点.
然后设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 得到。
得到。
(1)设 为曲线
为曲线 上的任意一点,则点
上的任意一点,则点 在圆
在圆 上,
上,
∴ ,曲线
,曲线 的方程为
的方程为 . ………………2分
. ………………2分
(2)设点 的坐标为
的坐标为 ,直线
,直线 的方程为
的方程为 , ………………3分
, ………………3分
代入曲线 的方程
的方程 ,可得
,可得  ,……5分
,……5分
∵ ,∴
,∴ ,
,
∴直线 与曲线
与曲线 总有两个公共点.(也可根据点M在椭圆
总有两个公共点.(也可根据点M在椭圆 的内部得到此结论)
的内部得到此结论)
………………6分
设点 ,
, 的坐标分别
的坐标分别 ,
,  ,则
,则 ,
,
要使 被
被 轴平分,只要
轴平分,只要 ,
………………9分
,
………………9分
即 ,
, , ………………10分
, ………………10分
也就是 ,
, ,
,
即 ,即只要
,即只要 ………………12分
………………12分
当 时,(*)对任意的s都成立,从而
时,(*)对任意的s都成立,从而 总能被
总能被 轴平分.
轴平分.
所以在x轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
已知 ,(其中
,(其中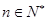 )
)
⑴求 及
及 ;
;
⑵试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
【解析】第一问中取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得
取 ,则
,则 得到结论
得到结论
第二问中,要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,归纳猜想可得结论当
的大小,归纳猜想可得结论当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
;
猜想:当 时,
时, 运用数学归纳法证明即可。
运用数学归纳法证明即可。
解:⑴取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得 ,
,
取 ,则
,则 。 …………4分
。 …………4分
⑵要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,
的大小,
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
…………6分
;
…………6分
猜想:当 时,
时, ,下面用数学归纳法证明:
,下面用数学归纳法证明:
由上述过程可知, 时结论成立,
时结论成立,
假设当 时结论成立,即
时结论成立,即 ,
,
当 时,
时,
而
∴
即 时结论也成立,
时结论也成立,
∴当 时,
时, 成立。
…………11分
成立。
…………11分
综上得,当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时,
已知数列 的前
的前 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求 的通项公式;
的通项公式;
(Ⅱ) 设 (
( N*).
N*).
①证明:  ;
;
② 求证: .
.
【解析】本试题主要考查了数列的通项公式的求解和运用。运用 关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到
关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到 ,②由于
,②由于 ,
,
所以 利用放缩法,从此得到结论。
利用放缩法,从此得到结论。
解:(Ⅰ)当 时,由
时,由 得
得 . ……2分
. ……2分
若存在 由
由 得
得 ,
,
从而有 ,与
,与 矛盾,所以
矛盾,所以 .
.
从而由 得
得 得
得 . ……6分
. ……6分
(Ⅱ)①证明:
证法一:∵ ∴
∴
∴
∴ .…………10分
.…………10分
证法二: ,下同证法一.
……10分
,下同证法一.
……10分
证法三:(利用对偶式)设 ,
, ,
,
则 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因为
,又因为 ,所以
,所以 .即
.即
 ………10分
………10分
证法四:(数学归纳法)①当 时,
时,  ,命题成立;
,命题成立;
②假设 时,命题成立,即
时,命题成立,即 ,
,
则当 时,
时,

 即
即
即
故当 时,命题成立.
时,命题成立.
综上可知,对一切非零自然数 ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于 ,
,
所以 ,
,
从而 .
.
也即
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com