题目列表(包括答案和解析)
C．选修4—4：坐标系与参数方程
(本小题满分10分)
在极坐标系中，圆
的方程为
，以极点为坐标原点，极轴为
轴的正半轴建立平面直角坐标系，直线
的参数方程为
（
为参数），判断直线和圆的位置关系．
C．选修4-4：坐标系与参数方程（本小题满分10分）
在平面直角坐标系
中，求过椭圆
（
为参数）的右焦点且与直线
（
为参数）平行的直线的普通方程。
C．（选修4—4：坐标系与参数方程）
在极坐标系中，圆
的方程为
，以极点为坐标原点，极轴为
轴的正
半轴建立平面直角坐标系，直线
的参数方程为
（
为参数），求直线被
截
得的弦
的长度.
C．（坐标系与参数方程选做题）已知极坐标的极点在直角坐标系的原点O处，极轴与x轴的正半轴重合，曲线C的参数方程为
（
为参数），直线l的极坐标方程为
．点P在曲线C上，则点P到直线l的距离的最小值为
．
C．选修4－4：坐标系与参数方程
在直角坐标系
中，已知曲线
的参数方程是
（
是参数），若以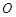
为极点，
轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线的极坐标方程．
一选择题：DAADB CBDDC
二.填空题：11. 1 ；
12.5 13. 
14. 1; 15.5
16．解：(1)
…………4分
将y=cos2x的图象先向左平移
个单位长度，再将所得图像上的点的横坐标保持不变，纵坐标伸长为原来的
倍，最后将所得图像向上平移2个单位即可.………………………………………………7分
(2)
…………9分
即
……………………11分
∴函数f(x)的最小值为3，最大值为
…………………………………………………12分
17．解：(1)
；……………………5分
由
，得
，
∴
的单调减区间是
；阶段 ………………8分
(2)当
时，
，
∴在
时，取最大值
，由
，得
。…………12分
18．解析：（1）
=
……
=
…………
（2）由余弦定理，得
即
……………………………………
……………………
可求得
…………………………………
19．解：（I） 公差为
，公比为
。
由条件：
，得
……………………4分
………………………………………………6分
（II）由（1）可知
……………………（1）
………………………（2）
由（2）-（1）得
…………………………9分
…………………………………………………………12分
20．解：（Ⅰ）该出版社一年的利润
（万元）与每本书定价
的函数关系式为：
．……………………4分（定义域不写扣2分）
（Ⅱ）
．…………………………6分
令
得
或x=20（不合题意，舍去）．…………7分
， 
．
在两侧
的值由正变负．
所以（1）当
即
时，
．……9分
（2）当
即
时，
，…………………………11分
所以
答：若，则当每本书定价为
元时，出版社一年的利润最大，最大值
（万元）；若，则当每本书定价为11元时，出版社一年的利润最大，最大值
（万元）．…………………………13分
21．解：（1）函数定义域为
………………………………2分
∵
由
∴增区间：（0，+∞），减区间：（－1，0）………………………………5分
（2）由
∵
……………………8分
∴
∴
时，
恒成立。………………………………………………10分
（3）
……………………11分
∵
由
，
故
上恰有两相异实根
……………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com