
题目列表(包括答案和解析)
| A.两列波速度可能都是3m/s |
| B.两列波在重叠时,x=10m处振动最强 |
| C.两列波在重叠时,x=15m处振动最弱 |
| D.两列波在重叠时,x=12.5m处振动最强 |
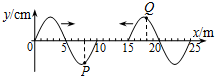

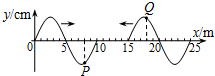 (2006?淮安二模)同一介质中的两列简谐横波分别沿x轴正方向和负方向传播,在t=0时刻的波形图如图所示.t=1s时,平衡位置在x=8m处的质点P刚好回到平衡位置.关于这两列波的下列说法中正确的是( )
(2006?淮安二模)同一介质中的两列简谐横波分别沿x轴正方向和负方向传播,在t=0时刻的波形图如图所示.t=1s时,平衡位置在x=8m处的质点P刚好回到平衡位置.关于这两列波的下列说法中正确的是( )(09年双鸭山一中期末)同一介质中的两列简谐横波分别沿x轴正方向和负方向传播,在t=0时刻的波形图如图所示。t=1s时,平衡位置在x=8m处的质点P刚好回到平衡位置。关于这两列波的下列说法中正确的是( )
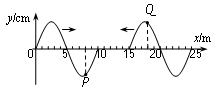
A.两列波速度可能都是3m/s
B.两列波在重叠时,x=10m处振动最强
C.两列波在重叠时,x=15m处振动最弱
D.两列波在重叠时,x=12.5m处振动最强
一、选择题(每题4分共40分)
1、B 2、D 3、B 4、ABD 5、B 6、ABD 7、C 8、ACD 9、AD 10、DC
二、实验题(两题共14分)
|