
题目列表(包括答案和解析)
已知函数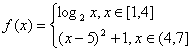
(1)在给定的直角坐标系内画出![]() 的图象;
的图象;
(2)写出![]() 的单调递增区间(不需要证明);
的单调递增区间(不需要证明);
(3)写出![]() 的最大值和最小值(不需要证明).
的最大值和最小值(不需要证明).
(第II卷) 50分
一、填空题(本大题共2小题,每小题4分,共8分.把答案填在答题卡上)
已知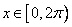 ,且
,且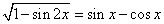 ,则 ( )
,则 ( )
A.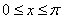 B.
B.
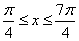
C. 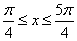 D.
D.

第II卷(非选择题,共60分)
设 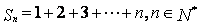 ,则
,则 的最大值.为( )
的最大值.为( )
A. B.
B.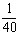 C. D.
C. D.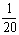
第II卷(非选择题 共70分)
已知奇函数![]() 在[-1,0]上为单调递减函数,又
在[-1,0]上为单调递减函数,又![]() 为锐角三角形两内角,则( )
为锐角三角形两内角,则( )
![]()
![]()
![]()
![]()
第II卷
设函数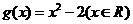 ,
, ,则
,则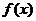 的值域是( )
的值域是( )
A. B.
B.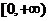 C.
C.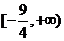 D.
D.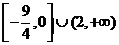
第II卷(非选择题,共90分)
一、选择题:本大题共12小题,每小题5分,共60分。
BBDD CABC BCDB
二、填空题:本大题共4小 题,每小题4分,共16分。
13.8500
14.
15.
16.①③
三、解答题:本大题共6小题,共74分。
17.解:(I)依题意,
由正弦定理及 3分
3分
 6分
6分
(II)由
由 (舍去负值) 8分
(舍去负值) 8分
从而, 9分
9分
由余弦定理,得
代入数值,得
解得 12分
12分
18.解:(I)随意抽取4件产品进行检查是随机事件,而第一天有9件正品,
第一天通过检查的概率为错误!嵌入对象无效。 2分
第二天通过检查的概率为 错误!嵌入对象无效。 4分
因为第一天、第二天检查是否通过是相互独立的,
所以两天全部通过检查的概率为错误!嵌入对象无效。 6分
(II)记所得奖金为 元,则
元,则 的取值为-300,300,900 7分
的取值为-300,300,900 7分


 10分
10分
 (元) 12分
(元) 12分
19.解:(I)如图,以AB,AC,AA1分别为 轴,建立空间直角坐标系
轴,建立空间直角坐标系
则 2分
2分
从而
所以 3分
3分
(II)平面ABC的一个法向量为
则
 (※) 5分
(※) 5分
而
由(※)式,当 6分
6分
(III)平面ABC的一个法向量为
设平面PMN的一个法向量为
由(I)得
由 7分
7分
解得 9分
9分
 平面PMN与平面ABC所成的二面角为45°,
平面PMN与平面ABC所成的二面角为45°,

解得 11分
11分
故点P在B1A1的延长线上,且 12分
12分
20.(本小题满发12分)
解:(I)由题设知 1分
1分
同时
两式作差得
所以
可见,数列
 4分
4分
(II) 5分
5分



 7分
7分
(III)
 9分
9分
①当
解得 符合题意,此时不存在符合题意的M。 10分
符合题意,此时不存在符合题意的M。 10分
②当
解得 此时存在的符合题意的M=8。 11分
此时存在的符合题意的M=8。 11分
综上所述,当 时,存在M=8符合题意 12分
时,存在M=8符合题意 12分
21.解:(I)因为
所以
因为 上是增函数。
上是增函数。
所以 上恒成立 1分
上恒成立 1分
当
而 上的最小值是-1。
上的最小值是-1。
于是 (※)
(※)
可见
从而由(※)式即得 ① 4分
① 4分
同时,
由
解得 ②,
②,
或
由①②得 
此时, 即为所求 6分
即为所求 6分
注:没有提到(验证) 时,
时, 不扣分。
不扣分。
(II)由(I),
于是 7分
7分
以下证明 (☆)
(☆)
(☆)等价于 8分
8分
构造函数
则 时,
时,
 上为增函数。
上为增函数。
因此当
即
从而 得到证明。 11分
得到证明。 11分
同理可证 12分
12分
注:没有“综上”等字眼的结论,扣1分。

即 2分
2分
由
则
所以 (※) 4分
(※) 4分
又因为
则
代入(※)式得

可见, 无关。 6分
无关。 6分
(II)如图,设
由(I)知 7分
7分
又
所以 8分
8分
将点A的坐标代入曲线C1的方程得
则 10分
10分
当且仅当“=”成立时,有 11分
11分
解得 14分
14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com