
题目列表(包括答案和解析)
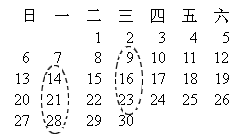
(2004·湖北黄冈)(1)在2004年6月的日历中(如图所示),任意圈出一竖列上相邻的三个数,设中间的一个为a,则用含a的代数式表示这三个数(从小到大排列)分别是________.
(2)现将连续自然数1~2 004按如图所示的方式排成一个长方形阵列,用一个正方形框出16个数.
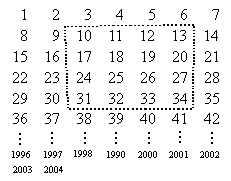
①图中框出的这16个数的和是________.
②在图中,要使一个正方形框出的16个数之和分别等于2 000,2 004,是否可能?若不可能,试说明理由;若有可能,请求出该正方形框出的16个数中的最小值和最大数.
 的一元二次方程
的一元二次方程
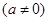 的两个实数根分别为
的两个实数根分别为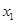 、
、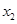 ,则
,则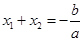 ,
, 
 有两个非零不等实数根
有两个非零不等实数根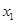 、
、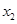 ,设
,设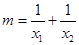 .
.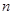 的取值范围;
的取值范围;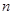 的代数式表示出
的代数式表示出 ;
; 值,使
值,使 的值等于1?若存在,求出这样的所有
的值等于1?若存在,求出这样的所有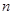 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. (本题8分)阅读下列材料:若关于 的一元二次方程
的一元二次方程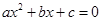
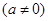 的两个实数根分别为
的两个实数根分别为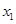 、
、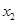 ,则
,则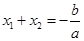 ,
, 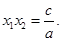
解决下面问题:已知关于x的一元二次方程 有两个非零不等实数根
有两个非零不等实数根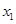 、
、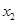 ,设
,设 .
.
【小题1】(1) 求 的取值范围;
的取值范围;
【小题2】(2) 试用关于 的代数式表示出
的代数式表示出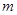 ;
;
【小题3】(3) 是否存在这样的 值,使
值,使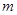 的值等于1?若存在,求出这样的所有
的值等于1?若存在,求出这样的所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 的一元二次方程
的一元二次方程
 的两个实数根分别为
的两个实数根分别为 、
、 ,则
,则 ,
, 
 有两个非零不等实数根
有两个非零不等实数根 、
、 ,设
,设 .
. 的取值范围;
的取值范围; 的代数式表示出
的代数式表示出 ;
; 值,使
值,使 的值等于1?若存在,求出这样的所有
的值等于1?若存在,求出这样的所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式P1P2=
在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式P1P2=| (x1-x2)2+(y1-y 2)2 |
| (-1-0)2+(2-3)2 |
| 2 |
| 13 |
| 13 |
| 13 |
| 13 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com