练习册

  • 练习册
  • 试题
    6．如图2.边长为的大正方形中剪去一个边长为的小正方形.小明将左图的阴影部分拼成右图的长方形.这一个过程可以验证的公式是 . 【查看更多】

     

    题目列表(包括答案和解析)

    如图，小明把一张长为20cm，宽为10cm的矩形硬纸板的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子．设剪去的正方形边长为x （cm），折成的长方体盒子的侧面积为y （cm2），底面积为S （cm2）．
    （1）求S与x之间的函数关系式，并求S=44 （cm2）时x的值；（结果可保留根式）
    （2）求y与x之间的函数关系式；在x的变化过程中，y会不会有最大值？x取何值时取得最大值，最大值是多少？
    精英家教网

    查看答案和解析>>

    如图，在边长为4的正方形纸片ABCD中，从边CD上剪去一个矩形EFGH，且有EF=DH=CE=1cm，FG=2cm，动点P从点A开始沿AD边向点D以1cm/s的速度运动至点D停止．以AP为边在AP的下方做正方形AQKP，设点P运动时间为t（s），正方形AQKP和纸片重叠部分的面积为S（cm2），则S与t之间的函数关系用图象表示大致是（　　）
    A、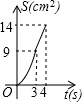B、C、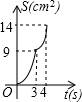D、

    查看答案和解析>>

    如图，在边长为24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体形状的包装盒（A．B．C．D四个顶点正好重合于上底面上一点）．已知E、F在AB边上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x（cm）．
    （1）若折成的包装盒恰好是个正方体，试求这个包装盒的体积V；
    （2）某广告商要求包装盒的表面（不含下底面）面积S最大，试问x应取何值？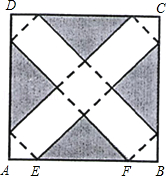

    查看答案和解析>>

    如图，在边长为24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体形状的包装盒（A、B、C、D四个顶点正好重合于上底面上一点）。已知E、F在ＡＢ边上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x(cm).

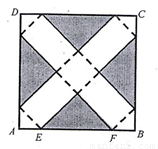
    （1）若折成的包装盒恰好是个正方体，试求这个包装盒的体积V；

    （2）某广告商要求包装盒的表面（不含下底面）面积S最大，试问x应取何值？S最大值是多少？

     

    查看答案和解析>>

    如图，在边长为24cm的正方形纸片ABCD上，剪去图中阴影部分的四个全等的等腰直角三角形，再沿图中的虚线折起，折成一个长方体形状的包装盒（A．B．C．D四个顶点正好重合于上底面上一点）．已知E、F在AB边上，是被剪去的一个等腰直角三角形斜边的两个端点，设AE=BF=x（cm）．

    （1）若折成的包装盒恰好是个正方体，试求这个包装盒的体积V；

    （2）某广告商要求包装盒的表面（不含下底面）面积S最大，试问x应取何值？

     

    查看答案和解析>>


    同步练习册答案