
题目列表(包括答案和解析)

| A、2.5 | ||
B、2
| ||
C、
| ||
D、
|
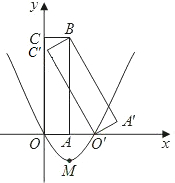 时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).
时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).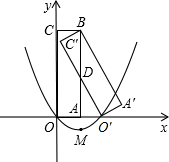 如图,矩形A′B′C′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).O′C′与AB交于D点.
如图,矩形A′B′C′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).O′C′与AB交于D点. 如图,矩形OABC的边OA在x轴正半轴上,边OC在y轴正半轴上,B点的坐标为(1,3).矩形O′A′BC′是矩形OABC绕B点逆时针旋转得到的.O′点恰好在x轴的正半轴上,O′C′交AB于点D.
如图,矩形OABC的边OA在x轴正半轴上,边OC在y轴正半轴上,B点的坐标为(1,3).矩形O′A′BC′是矩形OABC绕B点逆时针旋转得到的.O′点恰好在x轴的正半轴上,O′C′交AB于点D. 如图,矩形A′B′C′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).O′C′与AB交于D点.
如图,矩形A′B′C′O′是矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,O′点在x轴的正半轴上,B点的坐标为(1,3).O′C′与AB交于D点.一、选择题
1?D 2?A 3?C 4?A 5?C 6? B 7?C 8?B
二、填空题
9?y(x+2)(x-2) 10?x>5 11?4.37×1010 12?/数学.files/image132.gif) 13?-8
13?-8
14?y=x2-2x+1 15?4 16?/数学.files/image134.gif) 17?115° 18?
17?115° 18?/数学.files/image136.gif)
三、解答题
19.(1)原式=-1-1+2 ………………………(3分)
=0 ………………………(4分)
(2)x=-1………………………(3分)
检验………………………(4分)
20?化简得2x+4………………………(6分)
x 只能取2或3,取其余三个数错。………………………(8分)
21.(1)60 ………………………(2分)
18 ………………………(4分)
(2)第四组获奖率是/数学.files/image138.gif) ,第六组获奖率是
,第六组获奖率是/数学.files/image140.gif) ,
,/数学.files/image138.gif) <
</数学.files/image140.gif) ,
,
∴第六组获奖率高………………………(8分)
22?(1)DH=27.6………………………(4分)
(2)CD=5.0………………………(8分)
23?(1)略………………………(4分)
(2)略………………………(10分)
24?(1)公平………………………(4分)
(2)树状图或列表………………………(6分)
王伟获奖的概率是/数学.files/image144.gif) ………………………(7分)
………………………(7分)
张红获奖的概率是/数学.files/image138.gif) ………………………(8分)
………………………(8分)
/数学.files/image144.gif) <
</数学.files/image138.gif) ………………………(9分)
………………………(9分)
不公平………………………(10分)
25?(1)相切………………………(1分)
理由(略)………………………(4分)
不交待 “O是半径OA的外端”扣一分
(2)S=/数学.files/image148.gif)
26?(1)设高级教师招聘/数学.files/image090.gif) 人,则中级教师招聘
人,则中级教师招聘/数学.files/image151.gif) 人
人
求得13≤x≤15
/数学.files/image153.gif) ………………………(3分)
………………………(3分)
/数学.files/image155.gif) 学校对高级教师,中级教师有三种招聘方案
学校对高级教师,中级教师有三种招聘方案
/数学.files/image157.gif) ………………………(4分)
………………………(4分)
(2)当高级教师招聘13人,中级教师招聘27人时,学校所支付的月工资最少.????????? 7分
(3)补表:13、27??????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
在学校所支付的月工资最少时,中位数是2100元,众数是2000元?????????????????????????????? 12分
27.(1)略 ……2分
(2)不能……3 分
若PQ⊥BF时,/数学.files/image159.gif) ……5分,
……5分,
/数学.files/image161.gif) ,所以不能……6分
,所以不能……6分
(3)①BP=PQ,/数学.files/image163.gif) 或8(舍去)…8分
或8(舍去)…8分
②BQ=PQ, /数学.files/image165.gif) ……10分
……10分
③BP=BQ, 无解……12分
28.(1)/数学.files/image167.gif) ……3 分
……3 分
(2)D(1,/数学.files/image169.gif) ) ……7分
) ……7分
(3)tan/数学.files/image171.gif) =1或
=1或/数学.files/image173.gif) ……12分(求出一个得3分,求两个得5分)
……12分(求出一个得3分,求两个得5分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com