
题目列表(包括答案和解析)
求曲线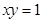 及直线
及直线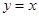 ,
,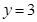 所围成的平面图形的面积.
所围成的平面图形的面积.
【解析】本试题主要是考查了定积分的运用。
解:做出曲线xy=1及直线y=x,y=3的草图,则所求面积为阴影部分的面积
解方程组 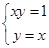 得直线y=x与曲线xy=1的交点坐标为(1,1)
得直线y=x与曲线xy=1的交点坐标为(1,1)
同理得:直线y=x与曲线y=3的交点坐标为(3,3)
直线y=3与曲线xy=1的交点坐标为(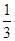 ,3)………………3分
,3)………………3分
因此,所求图形的面积为
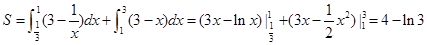
如图,测量河对岸的塔高 时,可以选与塔底
时,可以选与塔底 在同一水平面内的两个测点
在同一水平面内的两个测点 .现测得
.现测得
 ,并在点
,并在点 测得塔顶
测得塔顶 的仰角为
的仰角为 ,
求塔高
,
求塔高 (精确到
(精确到 ,
, )
)

【解析】本试题主要考查了解三角形的运用,利用正弦定理在 中,得到
中,得到 ,然后在
,然后在 中,利用正切值可知
中,利用正切值可知
解:在 中,
中,
由正弦定理得: ,所以
,所以 
在 中,
中,
在正方体 中,如图E、F分别是
中,如图E、F分别是
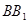 ,CD的中点,
,CD的中点,
(1)求证: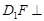 平面ADE;
平面ADE;
(2)cos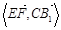 .
.
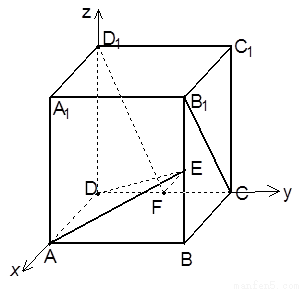
【解析】本试题主要考查了运用空间向量进行求证垂直问题和求解向量的夹角的余弦值的简单运用.
如图,在直三棱柱 中,底面
中,底面 为等腰直角三角形,
为等腰直角三角形, ,
, 为棱
为棱 上一点,且平面
上一点,且平面 平面
平面 .
.
(Ⅰ)求证: 点为棱
点为棱 的中点;
的中点;
(Ⅱ)判断四棱锥 和
和 的体积是否相等,并证明。
的体积是否相等,并证明。

【解析】本试题主要考查了立体几何中的体积问题的运用。第一问中,
易知 ,
, 面
面 。由此知:
。由此知: 从而有
从而有 又点
又点 是
是 的中点,所以
的中点,所以 ,所以
,所以 点为棱
点为棱 的中点.
的中点.
(2)中由A1B1⊥平面B1C1CD,BC⊥平面A1ABD,D为BB1中点,可以得证。
(1)过点 作
作 于
于 点,取
点,取 的中点
的中点 ,连
,连 。
。 面
面 面
面 且相交于
且相交于 ,面
,面 内的直线
内的直线 ,
, 面
面 。……3分
。……3分
又 面
面 面
面 且相交于
且相交于 ,且
,且 为等腰三角形,易知
为等腰三角形,易知 ,
, 面
面 。由此知:
。由此知: ,从而有
,从而有 共面,又易知
共面,又易知 面
面 ,故有
,故有 从而有
从而有 又点
又点 是
是 的中点,所以
的中点,所以 ,所以
,所以 点为棱
点为棱 的中点.
…6分
的中点.
…6分
(2)相等.ABC-A1B1C1为直三棱柱,∴BB1⊥A1B1,BB1⊥BC,又A1B1⊥B1C1,BC⊥AB,
∴A1B1⊥平面B1C1CD,BC⊥平面A1ABD(9分)∴VA1-B1C1CD=1 /3 SB1C1CD•A1B1=1/ 3 ×1 2 (B1D+CC1)×B1C1×A1B1VC-A1ABD=1 /3 SA1ABD•BC=1 /3 ×1 2 (BD+AA1)×AB×BC∵D为BB1中点,∴VA1-B1C1CD=VC-A1ABD
已知平面四边形 的对角线
的对角线 交于点
交于点 ,
,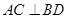 ,且
,且 ,
, ,
,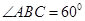 .现沿对角线
.现沿对角线 将三角形
将三角形 翻折,使得平面
翻折,使得平面 平面
平面 .翻折后:
(Ⅰ)证明:
.翻折后:
(Ⅰ)证明: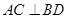 ;(Ⅱ)记
;(Ⅱ)记 分别为
分别为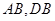 的中点.①求二面角
的中点.①求二面角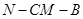 大小的余弦值;
②求点
大小的余弦值;
②求点 到平面
到平面 的距离
的距离
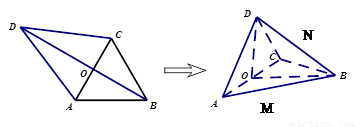

【解析】本试题主要考查了空间中点、线、面的位置关系的综合运用。以及线线垂直和二面角的求解的立体几何试题运用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com