如下图，过曲线C：y＝e^x上一点P₀(0，1)作曲线C的切线l₀交x轴于点Q₁(x₁，0)，又过Q₁作x轴的垂线交曲线C于点P₁(x₁，y₁)，然后再过P₁(x₁，y₁)作曲线C的切线l₁交x轴于点Q₂(x₂，0)，又过Q₂作x轴的垂线交曲线C于点P₂(x₂，y₂)，…，以此类推，过点P_n的切线l_n与x轴相交于点Q_n+1(x_n+1，0)，再过点Q_n+1作x轴的垂线交曲线C于点P_n+1(x_n+1，y_n+1)(n∈N^*)．

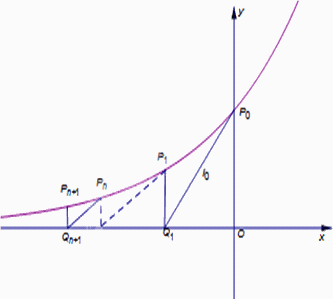
(1)求x₁、x₂及数列{x_n}的通项公式；

(2)设曲线C与切线l_n及直线P_n+1Q_n+1所围成的图形面积为S_n，求S_n的表达式；(3)在满足(2)的条件下，若数列{S_n}的前n项和为T_n，求证：N^*．

设满足以下两个条件的有穷数列a₁，a₂，…a_n为n(n＝2，3，4…)阶“期待数列”：

①a₁＋a₂＋a₃＋…＋a_n＝0；

②|a₁|＋|a₂|＋|a₃|＋…＋|a_n|＝1．

(1)若等比数列{a_n}为2k(k∈N*)阶“期待数列”，求公比q；

(2)若一个等差数列{a_n}既是2k(k∈N*)阶“期待数列”又是递增数列，求该数列的通项公式；

(3)记n阶“期待数列”{a_i}的前k项和为S_k(k＝1，2，3…，n)：

(ⅰ)求证：；

(ⅱ)若存在m∈{1，2，3…n}使，试问数列{S_i}能否为n阶“期待数列”？若能，求出所有这样的数列；若不能，请说明理由．

设满足以下两个条件的有穷数列a₁，a₂，…a_n为n(n＝2，3，4…)阶“期待数列”：

①a₁＋a₂＋a₃＋…＋a_n＝0；②|a₁|＋|a₂|＋|a₃|＋…＋|a_n|＝1．

(1)若等比数列{a_n}为2k(k∈N*)阶“期待数列”，求公比q；

(2)若一个等差数列{a_n}既是2k(k∈N*)阶“期待数列”又是递增数列，求该数列的通项公式；

(3)记n阶“期待数列”{a_i}的前k项和为S_k(k＝1，2，3，…n)：

(ⅰ)求证：；

(ⅱ)若存在m∈{1，2，3，…n}使，试问数列{S_i}能否为n阶“期待数列”？若能，求出所有这样的数列；若不能，请说明理由．