
题目列表(包括答案和解析)
设点 是抛物线
是抛物线

 的焦点,
的焦点, 是抛物线
是抛物线 上的
上的 个不同的点(
个不同的点(
 ).
).
(1) 当 时,试写出抛物线
时,试写出抛物线 上的三个定点
上的三个定点 、
、 、
、 的坐标,从而使得
的坐标,从而使得
 ;
;
(2)当 时,若
时,若 ,
,
求证: ;
;
(3) 当 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即:
“若 ,则
,则 .”
.”
开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
① 试构造一个说明该逆命题确实是假命题的反例(本研究方向最高得4分);
② 对任意给定的大于3的正整数 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
③ 如果补充一个条件后能使该逆命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由(本研究方向最高得10分).
【评分说明】本小题若填空不止一个研究方向,则以实得分最高的一个研究方向的得分作为本小题的最终得分.
【解析】第一问利用抛物线 的焦点为
的焦点为 ,设
,设 ,
,
分别过 作抛物线
作抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 .
.
由抛物线定义得到
第二问设 ,分别过
,分别过 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为 .
.
由抛物线定义得


第三问中①取 时,抛物线
时,抛物线 的焦点为
的焦点为 ,
,
设 ,
, 分别过
分别过
 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为
 .由抛物线定义得
.由抛物线定义得




 ,
,
则 ,不妨取
,不妨取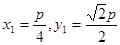 ;
;
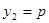 ;
;
 ;
;
解:(1)抛物线 的焦点为
的焦点为 ,设
,设 ,
,
分别过 作抛物线
作抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 .由抛物线定义得
.由抛物线定义得


因为 ,所以
,所以 ,
,
故可取

 满足条件.
满足条件.
(2)设 ,分别过
,分别过 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为 .
.
由抛物线定义得


 又因为
又因为



 ;
;
所以

 .
.
(3) ①取 时,抛物线
时,抛物线 的焦点为
的焦点为 ,
,
设 ,
, 分别过
分别过
 作抛物线
作抛物线 的准线
的准线 垂线,垂足分别为
垂线,垂足分别为
 .由抛物线定义得
.由抛物线定义得




 ,
,
则 ,不妨取
,不妨取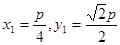 ;
;
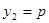 ;
;
 ;
; ,
,
则

 ,
,

 .
.
故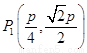 ,
, ,
, ,
, 是一个当
是一个当 时,该逆命题的一个反例.(反例不唯一)
时,该逆命题的一个反例.(反例不唯一)
② 设 ,分别过
,分别过 作
作
抛物线 的准线
的准线 的垂线,垂足分别为
的垂线,垂足分别为 ,
,
由 及抛物线的定义得
及抛物线的定义得
 ,即
,即 .
.
因为上述表达式与点 的纵坐标无关,所以只要将这
的纵坐标无关,所以只要将这 点都取在
点都取在 轴的上方,则它们的纵坐标都大于零,则
轴的上方,则它们的纵坐标都大于零,则






 ,
,
而 ,所以
,所以 .
.
(说明:本质上只需构造满足条件且 的一组
的一组 个不同的点,均为反例.)
个不同的点,均为反例.)
③ 补充条件1:“点 的纵坐标
的纵坐标 (
( )满足
)满足  ”,即:
”,即:
“当 时,若
时,若 ,且点
,且点 的纵坐标
的纵坐标 (
( )满足
)满足 ,则
,则 ”.此命题为真.事实上,设
”.此命题为真.事实上,设 ,
,
分别过 作抛物线
作抛物线 准线
准线 的垂线,垂足分别为
的垂线,垂足分别为 ,由
,由 ,
,
及抛物线的定义得 ,即
,即 ,则
,则






 ,
,
又由 ,所以
,所以 ,故命题为真.
,故命题为真.
补充条件2:“点 与点
与点
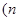 为偶数,
为偶数, 关于
关于 轴对称”,即:
轴对称”,即:
“当 时,若
时,若 ,且点
,且点 与点
与点
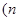 为偶数,
为偶数, 关于
关于 轴对称,则
轴对称,则 ”.此命题为真.(证略)
”.此命题为真.(证略)
(本小题满分12分)已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
,
(1)确定函数 的解析式;
的解析式;
(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)解不等式 .
.
【解析】第一问利用函数的奇函数性质可知f(0)=0
结合条件 ,解得函数解析式
,解得函数解析式
第二问中,利用函数单调性的定义,作差变形,定号,证明。
第三问中,结合第二问中的单调性,可知要是原式有意义的利用变量大,则函数值大的关系得到结论。
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米,
(I)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(II)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
(Ⅲ)若AN的长度不少于6米,则当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.

【解析】本题主要考查函数的应用,导数及均值不等式的应用等,考查学生分析问题和解决问题的能力 第一问要利用相似比得到结论。
(I)由SAMPN > 32 得 > 32 ,
> 32 ,
∵x >2,∴ ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴2<X<8/3,即AN长的取值范围是(2,8/3)或(8,+ )
)
第二问, 
当且仅当
(3)令
∴当x
> 4,y′> 0,即函数y= 在(4,+∞)上单调递增,∴函数y=
在(4,+∞)上单调递增,∴函数y= 在[6,+∞]上也单调递增.
在[6,+∞]上也单调递增.
∴当x=6时y= 取得最小值,即SAMPN取得最小值27(平方米).
取得最小值,即SAMPN取得最小值27(平方米).
设抛物线 :
: (
( >0)的焦点为
>0)的焦点为 ,准线为
,准线为 ,
, 为
为 上一点,已知以
上一点,已知以 为圆心,
为圆心, 为半径的圆
为半径的圆 交
交 于
于 ,
, 两点.
两点.
(Ⅰ)若 ,
, 的面积为
的面积为 ,求
,求 的值及圆
的值及圆 的方程;
的方程;
(Ⅱ)若 ,
, ,
, 三点在同一条直线
三点在同一条直线 上,直线
上,直线 与
与 平行,且
平行,且 与
与 只有一个公共点,求坐标原点到
只有一个公共点,求坐标原点到 ,
, 距离的比值.
距离的比值.
【命题意图】本题主要考查圆的方程、抛物线的定义、直线与抛物线的位置关系、点到直线距离公式、线线平行等基础知识,考查数形结合思想和运算求解能力.
【解析】设准线 于
于 轴的焦点为E,圆F的半径为
轴的焦点为E,圆F的半径为 ,
,

则|FE|= ,
, =
= ,E是BD的中点,
,E是BD的中点,
(Ⅰ) ∵ ,∴
,∴ =
= ,|BD|=
,|BD|= ,
,
设A( ,
, ),根据抛物线定义得,|FA|=
),根据抛物线定义得,|FA|= ,
,
∵ 的面积为
的面积为 ,∴
,∴ =
= =
= =
= ,解得
,解得 =2,
=2,
∴F(0,1), FA|= , ∴圆F的方程为:
, ∴圆F的方程为: ;
;
(Ⅱ) 解析1∵ ,
, ,
, 三点在同一条直线
三点在同一条直线 上, ∴
上, ∴ 是圆
是圆 的直径,
的直径, ,
,
由抛物线定义知 ,∴
,∴ ,∴
,∴ 的斜率为
的斜率为 或-
或- ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
设直线 的方程为:
的方程为: ,代入
,代入 得,
得, ,
,
∵ 与
与 只有一个公共点,
∴
只有一个公共点,
∴ =
= ,∴
,∴ ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
∴坐标原点到 ,
, 距离的比值为3.
距离的比值为3.
解析2由对称性设 ,则
,则
点 关于点
关于点 对称得:
对称得:
得: ,直线
,直线
 切点
切点
直线
坐标原点到 距离的比值为
距离的比值为
正方形ABCD的边长为1,点E在边AB上,点F在边BC上,AE=BF=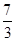 .动点P从E出发沿直线喜爱那个F运动,每当碰到正方形的方向的边时反弹,反弹时反射等于入射角,当点P第一次碰到E时,P与正方形的边碰撞的次数为
.动点P从E出发沿直线喜爱那个F运动,每当碰到正方形的方向的边时反弹,反弹时反射等于入射角,当点P第一次碰到E时,P与正方形的边碰撞的次数为
(A)16(B)14(C)12(D)10
【解析】结合已知中的点E,F的位置,进行作图,推理可知,在反射的过程中,直线是平行的,那么利用平行关系,作图,可以得到回到EA点时,需要碰撞14次即可.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com