
题目列表(包括答案和解析)
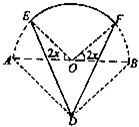 如图,实线部分DE,DF,EF是某风景区设计的游客观光路线平面图,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<
如图,实线部分DE,DF,EF是某风景区设计的游客观光路线平面图,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,∠EOA=∠FOB=2x(0<x<| π | 4 |
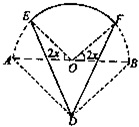 如图,实线部分DE,DF,EF是某风景区设计的游客观光路线平面图,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,
如图,实线部分DE,DF,EF是某风景区设计的游客观光路线平面图,其中曲线部分EF是以AB为直径的半圆上的一段弧,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,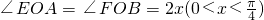 .若游客在每条路线上游览的“留恋度”均与相应的线段或弧的长度成正比,且“留恋度”与路线DE,DF的长度的比例系数为2,与路线EF的长度的比例系数为1,假定该风景区整体的“留恋度”y是游客游览所有路线“留恋度”的和.
.若游客在每条路线上游览的“留恋度”均与相应的线段或弧的长度成正比,且“留恋度”与路线DE,DF的长度的比例系数为2,与路线EF的长度的比例系数为1,假定该风景区整体的“留恋度”y是游客游览所有路线“留恋度”的和.在△ABC中,已知A(0,a),B(0,-a),AC、BC两边所在的直线分别与![]() 轴交于异于原点的点M和点N,且满足
轴交于异于原点的点M和点N,且满足![]() (a为不等于零的常数).
(a为不等于零的常数).
(Ⅰ)求点C的轨迹方程;
(Ⅱ)取a=2,是否存在斜率为2的直线l与点C的轨迹相交于不同的P、Q两点,且使△APQ为以点A为顶点的等腰三角形?若存在,求出直线的方程,若不存在,请说明理由.
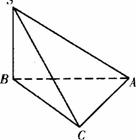
①异面直线SB与AC所成的角为90°;
②直线SB上平面ABC;
③二面角S-AC-B的大小为![]() ;
;
④点C到平面SAB的距离是![]() a.
a.
其中正确结论的序号是_____________.
 如图所示,ABCD是边长为a的正方形,△PBA是以角B为直角的等腰三角形,H为BD上一点,且AH⊥平面PDB.
如图所示,ABCD是边长为a的正方形,△PBA是以角B为直角的等腰三角形,H为BD上一点,且AH⊥平面PDB.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com