
题目列表(包括答案和解析)
| 1 |
| 3 |
| 1 |
| 6 |
| 21 |
| 4 |
| 23 |
| 4 |
| 4x+m2 |
| 2x |
| m2 |
| 9 |
 时,f(x)取得最大值2.
时,f(x)取得最大值2. )的单调递增区间,并指出该函数的图象可以由函数y=2sinx,x∈R的图象经过怎样的变换得到?
)的单调递增区间,并指出该函数的图象可以由函数y=2sinx,x∈R的图象经过怎样的变换得到?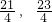 ]上是否存在f(x)的对称轴?如果存在,求出其对称轴方程;如果不存在,则说明理由.
]上是否存在f(x)的对称轴?如果存在,求出其对称轴方程;如果不存在,则说明理由.| 4x+m2 |
| 2x |
| m2 |
| 9 |
| 1 |
| 3 |
| 1 |
| 6 |
| 21 |
| 4 |
| 23 |
| 4 |
一、选择题:本大题共12小题,每小题5分,共60分.
1―5CADAD 6―10BACBC 11―12BD
二、填空题:本大题共4个小题,每小题4分,共16分.
13.--数学文科.files/image120.gif) 14.3 15.
14.3 15.--数学文科.files/image122.gif) 16.③④
16.③④
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
解:(I)由题意知--数学文科.files/image124.gif) ……………………1分
……………………1分
--数学文科.files/image126.gif)
--数学文科.files/image128.gif) ………………………………………………………6分
………………………………………………………6分
--数学文科.files/image130.gif)
--数学文科.files/image132.gif) ………………………………………………8分
………………………………………………8分
(II)--数学文科.files/image134.gif)
--数学文科.files/image136.gif) …………………………10分
…………………………10分
--数学文科.files/image138.gif)
--数学文科.files/image140.gif) 最大,其最大值为3.………………12分
最大,其最大值为3.………………12分
18.(本小题满分12分)
解证:设PA=1.
(I)由题意PA=BC=1,AD=2.……………………………………2分
--数学文科.files/image142.gif)
由勾股定理逆定理得AC⊥CD.……………………………………3分
又∵PA⊥面ABCD,CD--数学文科.files/image144.gif) 面ABCD,
面ABCD,
∴PA⊥CD. 又PA∩AC=A,∴CD⊥面PAC.……………………5分
又CD--数学文科.files/image144.gif) 面PCD,∴面PAD⊥面PCD.……………………6分
面PCD,∴面PAD⊥面PCD.……………………6分
(II)作CF∥AB交于AD于F,作EF∥AP交于PD于E,连接CE.……8分
--数学文科.files/image147.gif) ∵CF∥AB,EF∥PA,CF∩EF=F,PA∩AB=A,
∵CF∥AB,EF∥PA,CF∩EF=F,PA∩AB=A,
∴平面EFC∥平面PAB.………………10分
又CE--数学文科.files/image144.gif) 平面EFC,∴CE∥平面PAB.
平面EFC,∴CE∥平面PAB.
∵BC=--数学文科.files/image149.gif) ,AF=BC,
,AF=BC,
∴F为AD的中点,∴E为PD中点.
故棱PD上存在点E,且E为PD中点,使CE∥面PAB.……………………12分
19.(本小题满分12分)
解:(I)设捕捞n年后开始盈利,盈利为y元,
则--数学文科.files/image151.gif) …………3分
…………3分
当y>0时,得--数学文科.files/image153.gif)
解得--数学文科.files/image155.gif)
所以,该船捕捞3年后,开始盈利.……………………………………6分
(II)①年平均盈利为--数学文科.files/image157.gif) ,
,
当且仅当2n=--数学文科.files/image159.gif) ,即n=7时,年平均盈利最大.……………………8分
,即n=7时,年平均盈利最大.……………………8分
∴经过7年捕捞后年平均盈利最大,共盈利12×7+26=110万元.…………9分
②--数学文科.files/image161.gif) 的最大值为102.…11分
的最大值为102.…11分
∴经过10年捕捞后盈利总额达到最大,共盈利102+10=112万元.
故方案②较为合算.…………………………………………………………12分
20.(本小题满分12分)
解:(I)由题意知--数学文科.files/image163.gif)
--数学文科.files/image165.gif) 是等差数列.…………………………………………2分
是等差数列.…………………………………………2分
--数学文科.files/image167.gif)
--数学文科.files/image169.gif) ………………………………5分
………………………………5分
(II)由题设知--数学文科.files/image171.gif)
--数学文科.files/image173.gif)
--数学文科.files/image175.gif) 是等差数列.…………………………………………………………8分
是等差数列.…………………………………………………………8分
--数学文科.files/image177.gif)
--数学文科.files/image179.gif) ………………………………10分
………………………………10分
∴当n=1时,--数学文科.files/image181.gif) ;
;
当--数学文科.files/image183.gif)
经验证n=1时也适合上式. --数学文科.files/image185.gif) …………………………12分
…………………………12分
21.(本小题满分12分)
解:(I)--数学文科.files/image187.gif) 令
令--数学文科.files/image189.gif) …………………3分
…………………3分
当0<x<1时,--数学文科.files/image191.gif) 单调递增;
单调递增;
当--数学文科.files/image193.gif) 单调递减.
单调递减.
--数学文科.files/image195.gif) …………………………6分
…………………………6分
(II)由(I)知,当x=1时,--数学文科.files/image018.gif) 取得最大值,
取得最大值,
即--数学文科.files/image197.gif) …………………………………………………………8分
…………………………………………………………8分
由题意--数学文科.files/image112.gif) 恒成立,
恒成立,
--数学文科.files/image200.gif) ……………………………………………10分
……………………………………………10分
解得a>2或a<-1,即所求a的范围(-∞,-1)∪(2,+∞).…………12分
22.(本小题满分14分)
解:(I)由已知得--数学文科.files/image202.gif) 设
设--数学文科.files/image204.gif)
由--数学文科.files/image206.gif)
--数学文科.files/image208.gif) …………………………………………2分
…………………………………………2分
--数学文科.files/image210.gif)
--数学文科.files/image212.gif)
--数学文科.files/image214.gif) 同理
同理--数学文科.files/image216.gif) …………………………………………4分
…………………………………………4分
--数学文科.files/image218.gif) …………6分
…………6分
(II)当m=0时,A(1,--数学文科.files/image220.gif) ),B(1,-
),B(1,---数学文科.files/image220.gif) ),D(4,
),D(4,--数学文科.files/image220.gif) ),E(4,-
),E(4,---数学文科.files/image220.gif) ).
).
∵ABED为矩形,∴N(--数学文科.files/image222.gif) ………………8分
………………8分
当--数学文科.files/image224.gif)
--数学文科.files/image226.gif)
--数学文科.files/image228.gif) ∥
∥--数学文科.files/image230.gif) ,即A、N、E三点共线.……………………………………12分
,即A、N、E三点共线.……………………………………12分
同理可证,B、N、D三点共线.
综上,对任意m,直线AE、BD相交于定点--数学文科.files/image232.gif) …………………14分
…………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com