--数学理科.files/image153.jpg)
P(0,0,a),F(--数学理科.files/image155.gif) ,
,--数学理科.files/image155.gif) ,
,--数学理科.files/image155.gif) ).………………2分
).………………2分
(I)--数学理科.files/image157.gif)
--数学理科.files/image159.gif) …………………………………………4分
…………………………………………4分
--数学理科.files/image161.gif) (II)设平面DEF的法向量为
(II)设平面DEF的法向量为--数学理科.files/image163.gif)
得--数学理科.files/image165.gif)
取x=1,则y=-2,z=1.
--数学理科.files/image167.gif) ………………………………………………6分
………………………………………………6分
--数学理科.files/image169.gif)
设DB与平面DEF所成角为--数学理科.files/image171.gif) ……………………………………8分
……………………………………8分
(III)假设存在点G满足题意
因为--数学理科.files/image173.gif)
--数学理科.files/image175.gif)
∴存在点G,其坐标为(--数学理科.files/image155.gif) ,0,0),即G点为AD的中点.……………………12分
,0,0),即G点为AD的中点.……………………12分
19.(本小题满分12分)
解:(I)ξ的所有可能取值为0,1,2,依题意得:
--数学理科.files/image178.gif) …………3分
…………3分
∴ξ的分布列为
ξ
0
1
2
P
--数学理科.files/image180.gif)
--数学理科.files/image182.gif)
--数学理科.files/image180.gif)
∴Eξ=0×--数学理科.files/image180.gif) +1×
+1×--数学理科.files/image182.gif) +2×
+2×--数学理科.files/image180.gif) =1.…………………………………………4分
=1.…………………………………………4分
(II)设“甲、乙都不被选中”的事件为C,则--数学理科.files/image184.gif) ……6分
……6分
∴所求概率为--数学理科.files/image186.gif) …………………………………8分
…………………………………8分
(III)记“男生甲被选中”为事件A,“女生乙被选中”为事件B,
--数学理科.files/image188.gif) ………………………………10分
………………………………10分
--数学理科.files/image190.gif) ……………12分
……………12分
20.(本小题满分12分)
解:(I)由题意知--数学理科.files/image192.gif)
--数学理科.files/image194.gif) 是等差数列.…………………………………………2分
是等差数列.…………………………………………2分
--数学理科.files/image196.gif)
--数学理科.files/image198.gif) ………………………………5分
………………………………5分
(II)由题设知--数学理科.files/image200.gif)
--数学理科.files/image202.gif)
--数学理科.files/image204.gif) 是等差数列.…………………………………………………………8分
是等差数列.…………………………………………………………8分
--数学理科.files/image206.gif)
--数学理科.files/image208.gif) ………………………………10分
………………………………10分
∴当n=1时,--数学理科.files/image210.gif) ;
;
当--数学理科.files/image212.gif)
经验证n=1时也适合上式. --数学理科.files/image214.gif) …………………………12分
…………………………12分
21.(本小题满分12分)
解:(I)令--数学理科.files/image216.gif)
则--数学理科.files/image218.gif)
--数学理科.files/image220.gif) 是单调递减函数.……………………………………2分
是单调递减函数.……………………………………2分
又取--数学理科.files/image222.gif)
--数学理科.files/image224.gif) 在其定义域上有唯一实根.……………………………4分
在其定义域上有唯一实根.……………………………4分
(II)由(I)知方程--数学理科.files/image111.gif) 有实根(或者由
有实根(或者由--数学理科.files/image111.gif) ,易知x=0就是方程的一个根),
,易知x=0就是方程的一个根),--数学理科.files/image068.gif) 满足条件①.………………………………………………5分
满足条件①.………………………………………………5分
--数学理科.files/image227.gif)
--数学理科.files/image229.gif) 满足条件②.故
满足条件②.故--数学理科.files/image068.gif) 是集合M中的元素.……………………………7分
是集合M中的元素.……………………………7分
(III)不妨设--数学理科.files/image231.gif) 在其定义域上是增函数.
在其定义域上是增函数.
--数学理科.files/image233.gif) ………………………………………………………………8分
………………………………………………………………8分
--数学理科.files/image235.gif) 是其定义域上的减函数.
是其定义域上的减函数.
--数学理科.files/image237.gif) .………………10分
.………………10分
--数学理科.files/image239.gif)
--数学理科.files/image241.gif) …………………………………………12分
…………………………………………12分
22.(本小题满分14分)
解:(I)设--数学理科.files/image243.gif)
由--数学理科.files/image245.gif)
--数学理科.files/image247.gif) ………………………………………………2分
………………………………………………2分
又--数学理科.files/image249.gif)
--数学理科.files/image251.gif)
同理,由--数学理科.files/image253.gif) ………………………………4分
………………………………4分
--数学理科.files/image255.gif) …………6分
…………6分
(II)方法一:当m=0时,A(2,2--数学理科.files/image004.gif) ),B(2,-
),B(2,---数学理科.files/image004.gif) ),D(n,2
),D(n,2--数学理科.files/image004.gif) ),E(n,-2
),E(n,-2--数学理科.files/image004.gif) ).
).
∵ABED为矩形,∴直线AE、BD的交点N的坐标为(--数学理科.files/image257.gif) ………………8分
………………8分
当--数学理科.files/image259.gif)
--数学理科.files/image261.gif)
同理,对--数学理科.files/image263.gif) 、
、--数学理科.files/image265.gif) 进行类似计算也得(*)式.………………………………12分
进行类似计算也得(*)式.………………………………12分
即n=-2时,N为定点(0,0).
反之,当N为定点,则由(*)式等于0,得n=-2.…………………………14分
方法二:首先n=-2时,则D(-2,y1),A(--数学理科.files/image267.gif)
--数学理科.files/image269.gif) ①
①
--数学理科.files/image271.gif) ②…………………………………………8分
②…………………………………………8分
①-②得--数学理科.files/image273.gif)
--数学理科.files/image275.gif)
--数学理科.files/image277.gif) …………………………………………………………10分
…………………………………………………………10分
反之,若N为定点N(0,0),设此时--数学理科.files/image279.gif)
则--数学理科.files/image281.gif)
由D、N、B三点共线,--数学理科.files/image283.gif) ③
③
同理E、N、A三点共线,--数学理科.files/image285.gif) ④………………12分
④………………12分
③+④得--数学理科.files/image287.gif)
即-16m+8m-4m=0,m(n+2)=0.
故对任意的m都有n=-2.……………………………………………………14分

 时,f(x)取得最大值2.
时,f(x)取得最大值2. )的单调递增区间,并指出该函数的图象可以由函数y=2sinx,x∈R的图象经过怎样的变换得到?
)的单调递增区间,并指出该函数的图象可以由函数y=2sinx,x∈R的图象经过怎样的变换得到?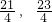 ]上是否存在f(x)的对称轴?如果存在,求出其对称轴方程;如果不存在,则说明理由.
]上是否存在f(x)的对称轴?如果存在,求出其对称轴方程;如果不存在,则说明理由.--数学理科.files/image129.gif) 14.
14.--数学理科.files/image131.gif) 15.
15.--数学理科.files/image133.gif) 16.③④
16.③④--数学理科.files/image135.gif) ……………………1分
……………………1分--数学理科.files/image137.gif)
--数学理科.files/image139.gif) ………………………………………………………6分
………………………………………………………6分--数学理科.files/image141.gif)
--数学理科.files/image143.gif) ………………………………………………8分
………………………………………………8分--数学理科.files/image145.gif)
--数学理科.files/image147.gif) …………………………10分
…………………………10分--数学理科.files/image149.gif)
--数学理科.files/image151.gif) 最大,其最大值为3.………………12分
最大,其最大值为3.………………12分