练习册

  • 练习册
  • 试题
    如图.在四棱锥P―ABCD中.PD⊥底面ABCD.底面ABCD为正方形.PD=DC.E.F分别是AB.PB的中点. (I)求证:EF⊥CD, (II)求DB与平面DEF所成角的正弦值, (III)在平面PAD内是否存在一点G.使G在平面PCB上的射影为△PCB的外心.若存在.试确定点G的位置,若不存在.说明理由. 【查看更多】

     

    题目列表(包括答案和解析)

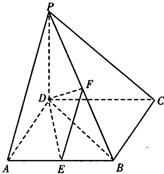    精英家教网如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC=1，E、F分别是AB、PB的中点．
    （Ⅰ）求证：EF⊥CD；
    （Ⅱ）求二面角F-DE-B的大小；
    （Ⅲ）在平面PAD内求一点G，使GF⊥平面PCB，并证明你的结论．

    查看答案和解析>>

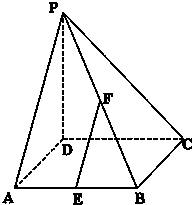    精英家教网如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E，F分别是AB，PB的中点．
    （Ⅰ）求证：EF∥平面PAD；
    （Ⅱ）求证：EF⊥CD；
    （Ⅲ）若G是线段AD上一动点，试确定G点位置，使GF⊥平面PCB，并证明你的结论．

    查看答案和解析>>

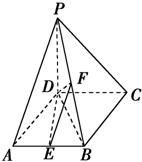    精英家教网如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E、F分别是AB、PB的中点．
    （1）求证：EF⊥CD；
    （2）求DB与平面DEF所成角的正弦值．

    查看答案和解析>>

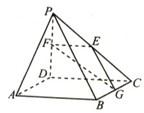    精英家教网如图，在四棱锥P-ABCD中，PD⊥底面ABCD，且底面ABCD为正方形，AD=PD=2，E，F，G分别为PC，PD，CB的中点．
    （1）求证：AP∥平面EFG；
    （2）求二面角G-EF-D的大小；
    （3）求三棱锥C-PAB的体积．

    查看答案和解析>>

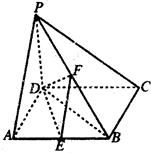    20、如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E、F分别是AB、PB的中点．
    （1）求证：CD∥面PAB；
    （2）求异面直线EF与CD所成角；
    （3）在AD上是否存在点Q，使QF⊥面PBC，给出理由或证明．

    查看答案和解析>>

    一、选择题：本大题共12小题，每小题5分，共60分.

    1―5CADAD   6―10BACBC   11―12BD

    二、填空题：本大题共4个小题，每小题4分，共16分.

    13．  14．  15． 16．③④

    三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤.

    17．（本小题满分12分）

           解：（I）由题意知……………………1分

          

           ………………………………………………………6分

          

           ………………………………………………8分

       （II）

           …………………………10分

          

           最大，其最大值为3.………………12分

    18．（本小题满分12分）

           解：以DA，DC，DP所在直线分别为x轴，y轴，z轴建立空间直角坐标系（如图）.

           P（0，0，a），F（，，）.………………2分

       （I）

           …………………………………………4分

    文本框:    （II）设平面DEF的法向量为

           得

           取x=1，则y=－2，z=1.

           ………………………………………………6分

          

           设DB与平面DEF所成角为……………………………………8分

       （III）假设存在点G满足题意

           因为

          

           ∴存在点G，其坐标为（，0，0），即G点为AD的中点.……………………12分

    19．（本小题满分12分）

           解：（I）ξ的所有可能取值为0，1，2，依题意得：

           …………3分

           ∴ξ的分布列为

          

    ξ

    0

    1

    2

    P

           ∴Eξ=0×+1×+2×=1.…………………………………………4分

       （II）设“甲、乙都不被选中”的事件为C，则……6分

           ∴所求概率为…………………………………8分

       （III）记“男生甲被选中”为事件A，“女生乙被选中”为事件B，

           ………………………………10分

           ……………12分

    20．（本小题满分12分）

           解：（I）由题意知

           是等差数列.…………………………………………2分

          

           ………………………………5分

       （II）由题设知

          

           是等差数列.…………………………………………………………8分

          

           ………………………………10分

           ∴当n=1时，；

           当

           经验证n=1时也适合上式. …………………………12分

    21．（本小题满分12分）

           解：（I）令

           则

           是单调递减函数.……………………………………2分

           又取

           在其定义域上有唯一实根.……………………………4分

       （II）由（I）知方程有实根（或者由，易知x=0就是方程的一个根），满足条件①.………………………………………………5分

          

           满足条件②.故是集合M中的元素.……………………………7分

       （III）不妨设在其定义域上是增函数.

           ………………………………………………………………8分

           是其定义域上的减函数.

           .………………10分

          

           …………………………………………12分

    22．（本小题满分14分）

           解：（I）设

           由

           ………………………………………………2分

           又

          

           同理，由………………………………4分

           …………6分

       （II）方法一：当m=0时，A（2，2），B（2，－），D（n，2），E（n，－2）.

           ∵ABED为矩形，∴直线AE、BD的交点N的坐标为（………………8分

           当

          

           同理，对、进行类似计算也得（*）式.………………………………12分

           即n=－2时，N为定点（0，0）.

           反之，当N为定点，则由（*）式等于0，得n=－2.…………………………14分

           方法二：首先n=－2时，则D（－2，y1），A（

             ①

             ②…………………………………………8分

           ①－②得

          

           …………………………………………………………10分

           反之，若N为定点N（0，0），设此时

           则

           由D、N、B三点共线，   ③

           同理E、N、A三点共线， ④………………12分

           ③+④得

           即－16m+8m－4m=0，m(n+2)=0.

           故对任意的m都有n=－2.……………………………………………………14分

     

     

     


    同步练习册答案