
题目列表(包括答案和解析)
在一个2×2列联表中,由其数据计算得K2的观测值k=13.097,则两个变量X与Y有关系的可能性为
99.9%
95%
90%
无关系
在一个2×2列联表中,由其数据计算得k2=13.097,则其两个变量间有关系的可能性为
A.99%
B.95%
C.90%
D.无关系
下列命题中正确的有
①设有一个回归方程 =2—3x,变量x增加一个单位时,y平均增加3个单位;
=2—3x,变量x增加一个单位时,y平均增加3个单位;
②命题P:“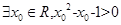 ”的否定
”的否定 P:“
P:“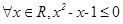 ”;
”;
③设随机变量X服从正态分布N(0,1),若P(X>1)=p,则P(-1<X<0)= -p;
-p;
④在一个2×2列联表中,由计算得k2=6.679,则有99%的把握确认这两个变量间有关系.
A.1个 B.2个 C.3个 D.4个
本题可以参考独立性检验临界值表
|
P(K2≥k) |
0.5 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.535 |
7.879 |
10.828 |
一、选择题:(每题5分,共60分)
|