
题目列表(包括答案和解析)
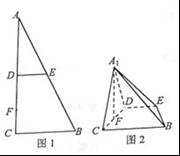
如图1,在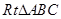 中,
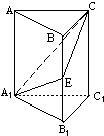
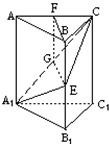
中,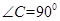 ,D,E分别为AC,AB的中点,点F为线段CD上的一点,将
,D,E分别为AC,AB的中点,点F为线段CD上的一点,将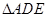 沿DE折起到
沿DE折起到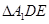 的位置,使
的位置,使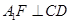 ,如图2.
,如图2.
(Ⅰ)求证:DE∥平面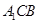
(Ⅱ)求证: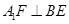
(Ⅲ)线段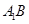 上是否存在点Q,使
上是否存在点Q,使 ?说明理由。
?说明理由。
【解析】(1)∵DE∥BC,由线面平行的判定定理得出
(2)可以先证 ,得出
,得出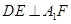 ,∵
,∵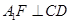 ∴
∴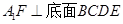
∴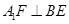
(3)Q为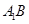 的中点,由上问
的中点,由上问 ,易知
,易知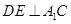 ,取
,取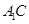 中点P,连接DP和QP,不难证出
中点P,连接DP和QP,不难证出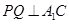 ,
,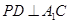 ∴
∴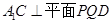 ∴
∴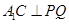 ,又∵
,又∵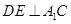 ∴
∴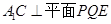
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
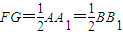 ,即
,即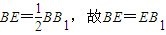 .
.如图,边长为2的正方形ABCD,E是BC的中点,沿AE,DE将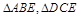 折起,使得B与C重合于O.
折起,使得B与C重合于O.
(Ⅰ)设Q为AE的中点,证明:QD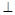 AO;
AO;
(Ⅱ)求二面角O—AE—D的余弦值.
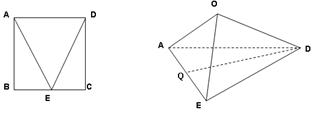
【解析】第一问中,利用线线垂直,得到线面垂直,然后利用性质定理得到线线垂直。取AO中点M,连接MQ,DM,由题意可得:AO EO, DO
EO, DO EO,
EO,
AO=DO=2.AO DM
DM
因为Q为AE的中点,所以MQ//E0,MQ AO
AO
AO 平面DMQ,AO
平面DMQ,AO DQ
DQ
第二问中,作MN AE,垂足为N,连接DN
AE,垂足为N,连接DN
因为AO EO, DO
EO, DO EO,EO
EO,EO 平面AOD,所以EO
平面AOD,所以EO DM
DM
,因为AO DM ,DM
DM ,DM 平面AOE
平面AOE
因为MN AE,DN
AE,DN AE,
AE,  DNM就是所求的DM=
DNM就是所求的DM= ,MN=
,MN=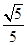 ,DN=
,DN= ,COS
,COS DNM=
DNM=
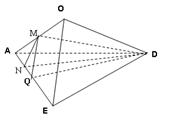
(1)取AO中点M,连接MQ,DM,由题意可得:AO EO, DO
EO, DO EO,
EO,
AO=DO=2.AO DM
DM
因为Q为AE的中点,所以MQ//E0,MQ AO
AO
AO 平面DMQ,AO
平面DMQ,AO DQ
DQ
(2)作MN AE,垂足为N,连接DN
AE,垂足为N,连接DN
因为AO EO, DO
EO, DO EO,EO
EO,EO 平面AOD,所以EO
平面AOD,所以EO DM
DM
,因为AO DM ,DM
DM ,DM 平面AOE
平面AOE
因为MN AE,DN
AE,DN AE,
AE,  DNM就是所求的DM=
DNM就是所求的DM= ,MN=
,MN=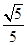 ,DN=
,DN= ,COS
,COS DNM=
DNM=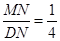
二面角O-AE-D的平面角的余弦值为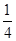
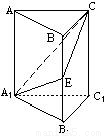
如图,四棱锥S—ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB
(Ⅰ)证明:平面EDC⊥平面SBC.(Ⅱ)求二面角A—DE—C的大小 .
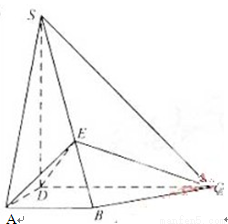
【解析】本试题主要考查了立体几何中的运用。
(1)证明:因为SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的三等分点,SE=2EB 所以ED⊥BS,DE⊥EC,所以ED⊥平面SBC.,因此可知得到平面EDC⊥平面SBC.
(Ⅱ)由SA2= SD2+AD2 = 5 ,AB=1,SE=2EB,AB⊥SA,知
AE2= (1 /3 SA)2+(2/ 3 AB)2 =1,又AD=1.
故△ADE为等腰三角形.
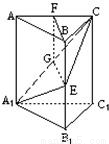
取ED中点F,连接AF,则AF⊥DE,AF2= AD2-DF2 =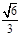 .
.
连接FG,则FG∥EC,FG⊥DE.
所以,∠AFG是二面角A-DE-C的平面角.
连接AG,AG= 2 ,FG2= DG2-DF2
=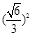 ,
,
cos∠AFG=(AF2+FG2-AG2 )/2⋅AF⋅FG =-1 /2 ,
所以,二面角A-DE-C的大小为120°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com