
题目列表(包括答案和解析)
(本小题12分)
某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其
初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为![]() ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)
(I)求甲选手回答一个问题的正确率;
(Ⅱ)求选手甲可进入决赛的概率;
(Ⅲ)设选手甲在初赛中答题的个数为![]() ,试写出
,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望。
的数学期望。
(本小题12分)
某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其
初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为![]() ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)
(I)求甲选手回答一个问题的正确率;
(Ⅱ)求选手甲可进入决赛的概率;
(Ⅲ)设选手甲在初赛中答题的个数为![]() ,试写出
,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望。
的数学期望。
(本小题满分12分)某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为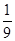 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为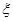 ,试写出
,试写出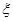 的分布列,并求
的分布列,并求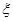 的数学期望。
的数学期望。
(本小题满分12分)某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有![]() 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对![]() 题或答错
题或答错![]() 题即终止其初赛的比赛:答对
题即终止其初赛的比赛:答对![]() 题者直接进入决赛,答错
题者直接进入决赛,答错![]() 题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为
题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为![]() .
.
⑴求选手甲可进入决赛的概率;
⑵设选手甲在初赛中答题的个数为![]() ,试求
,试求![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
(本小题满分12分)某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有![]() 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对![]() 题或答错
题或答错![]() 题即终止其初赛的比赛:答对
题即终止其初赛的比赛:答对![]() 题者直接进入决赛,答错
题者直接进入决赛,答错![]() 题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为
题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为![]() .
.
⑴求选手甲可进入决赛的概率;
⑵设选手甲在初赛中答题的个数为![]() ,试求
,试求![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
D
C
C
B
C
B
B
D
二、填空题
11.100 12.4 13.(-2,2) 14.
15. 16.
16. 17.
17.
18.(本小题14分)
解答:(1)设甲选手答对一个问题的正确率为 ,则
,则
故甲选手答对一个问题的正确率 3分
3分
(Ⅱ)选手甲答了3道题目进入决赛的概率为 =
= 4分
4分
选手甲答了4道题目进入决赛的概率为 5分
5分
选手甲答了5道题目进入决赛的概率为 6分
6分
选手甲可以进入决赛的概率 8分
8分
(Ⅲ) 可取3,4,5
可取3,4,5
则有 9分
9分
 10分
10分
 11分
11分
因此有 (直接列表也给分)

3
4
5




故 14分
14分
19.解:由三视图知,该多面体是低面为直角三角形的直三棱柱


(1)证明:连续取 ,易见
,易见 通过点
通过点 ,连接
,连接 。
。
 4分
4分
(2)作 于
于 ,连接
,连接
面


 故
故 为所求二面角的平面角。 6分
为所求二面角的平面角。 6分
在 中
中
故所求二面角的余弦值为 9分
9分
(3)棱锥 的体积
的体积 14分
14分
20 解:(1)解方程得 或
或 1分
1分
 当
当 时,
时, 或
或 ,此时
,此时 2分
2分
当 时,
时, 3分
3分
依次类推:
 5分
5分
(2)

 9分
9分
(3)由 得
得


 11分
11分
设
易证 在
在 上单调递减,在(
上单调递减,在( )上单调递增。 13分
)上单调递增。 13分



 15分
15分
21.解:(1)设 由
由 得
得
直线 的方程为:
的方程为:
直线 的方程为:
的方程为:
解方程组得 3分
3分
 由已知,
由已知, 三点共线,设直线
三点共线,设直线 的方程为:
的方程为:
与抛物线方程 联立消
联立消 可得:
可得:
 5分
5分
所以 点的纵坐标为-2,所以线段
点的纵坐标为-2,所以线段 中点的纵坐标O
中点的纵坐标O
即线段 被
被 轴平分。
6分
轴平分。
6分
(2)


=0 9分



 13分
13分
 而
而  所以在直角
所以在直角 中,
中,
由影射定理即得 15分
15分
22.解:(1) 代入得
代入得
设 1分
1分

 3分
3分
令 解得
解得
 在
在 上单调递减,在
上单调递减,在 上单调递增。 5分
上单调递增。 5分
 即原式的最小值为-1
7分
即原式的最小值为-1
7分
(2)要证 即证
即证
即证
即证 9分
9分
由已知 设
设 10分
10分
 11分
11分


 13分
13分
所以 在
在 上单调递减,
上单调递减, 
原不等式得证。 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com