练习册

  • 练习册
  • 试题
    【查看更多】

     

    题目列表(包括答案和解析)

    （）（本小题满分12分）

    如图，四棱锥S-ABCD 的底面是正方形，每条侧棱的长都是地面边长的倍，P为侧棱SD上的点。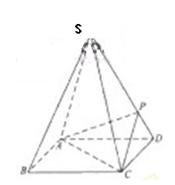   

    （Ⅰ）求证：AC⊥SD；

    （Ⅱ）若SD⊥平面PAC，求二面角P-AC-D的大小

    （Ⅲ）在（Ⅱ）的条件下，侧棱SC上是否存在一点E，使得BE∥平面PAC。若存在，求SE：EC的值；若不存在，试说明理由。

    查看答案和解析>>

    如下图，矩形ABCD，|AB|=1，|BC|=a，PA⊥平面ABCD，|PA|=1。

    （1）BC边上是否存在点Q，使得PQ⊥QD，并说明理由；

    （2）若BC边上存在唯一的点Q使得PQ⊥QD，指出点Q的位置，并求出此时AD与平面

    PDQ所成的角的正弦值；

    （3）在（2）的条件下，求二面角Q―PD―A的正弦值。

    查看答案和解析>>

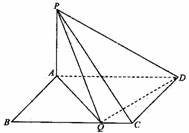
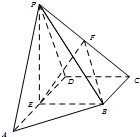    （2013•房山区一模）在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，ABCD为直角梯形，BC∥AD，∠ADC=90°，BC=CD=
    12
    AD=1    ，PA=PD，E，F为AD，PC的中点．
    （Ⅰ）求证：PA∥平面BEF；
    （Ⅱ）若PC与AB所成角为45°，求PE的长；
    （Ⅲ）在（Ⅱ）的条件下，求二面角F-BE-A的余弦值．

    查看答案和解析>>

    （本题满分12分）

    在三棱柱ABC-A1B1C1中，∠ACB=，AC=CB=1，D1是线段A1B1上一动点（可以与A1或B1重合）。过D1和CC1的平面与AB交于D。

    (1）若四边形CDD1C1总是矩形，求证：三棱柱ABC-A1B1C1为直三棱柱；

    (2)在（1）的条件下，求二面角B-AD1-C的取值范围。

       

     

    查看答案和解析>>

    在正四棱锥S—ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE⊥AC.

    （1）指出动点P的轨迹（即说明动点P在满足给定的条件下运动时所形成的图形），证明你的结论;

    （2）以轨迹上的动点P为顶点的三棱锥P－CDE的最大体积是正四棱锥S—ABCD体积的几分之几？

    （3）设动点P在G点的位置时三棱锥P－CDE的体积取最大值V1，二面角G—DE—C的大小为α，二面角G—CE—D的大小为β，求tanα∶tanβ的值；

    （4）若将“E是BC的中点”改为“E是BC上异于B、C的一定点”，其他条件不变，请指出点P的轨迹，证明你的结论.

    查看答案和解析>>

    一、选择题  1--5 DDCBA  6--10 ADBCA  11-12 AB

    二、填空题   13．     14．12   15．   16．AC          

    三、解答题

    17.解：（Ⅰ） ，

    ，

    ．   ，

    ，  ．

    （Ⅱ）由余弦定理，得　．

    ，  ．

    所以的最小值为，当且仅当时取等号．

    18、（Ⅰ）解法一：依据题意，因为队伍从水路或陆路抵达灾区的概率相等，则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C，且B、C相互独立，而且．……………………………………  2分

    在5月13日恰有1支队伍抵达灾区的概率是

    . ………………   5分

    解法二：在5月13日恰有1支队伍抵达灾区的概率是

    　　　　　 .………………………………………………………………  5分

    （Ⅱ）依据题意，因为队伍从水路或陆路抵达灾区的概率相等，则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C，且B、C相互独立，而且.

    设5月13日抵达灾区的队伍数为，则=0、1、2、3、4. ………………  6分

    由已知有：；…………………………………  7分

    ；…………………………  8分

    ；…………………  9分

    ；……………………… 10分

    . …………………………………………………  10分

    因此其概率分布为：

     

    0

    1

    2

    3

    4

    P

                                                            ………………  11分

    所以在5月13日抵达灾区的队伍数的数学期望为：

    =0×+ 1× + 2× + 3×+ 4×=.

    答：在5月13日抵达灾区的队伍数的数学期望=. ………………  12分

    19.（I）由已知a2－a１=－2, a3－a2=－1, －1－（－2）=1 ∴an+1－an=（a2－a1）+（n－1）?1=n－3 

    n≥2时，an=（ an－an－1）+（ an－1－an－2）+…+（ a3－a2）+（ a2－a1）+ a1

              =（n－4）+（n－5） +…+（－1）+（－2）+6 =

    n=1也合适.  ∴an=  （n∈N*） ……………………3分

    又b1－2=4、b2－2=2 .而  ∴bn－2=（b1－2）?（）n－1即bn=2+8?（）n

    ∴数列{an}、{bn}的通项公式为：an= ，bn=2+（）n－3……………  6分

    （II）设

    当k≥4时为k的增函数，－8?（）k也为k的增函数，……………  8分

    学科网(Zxxk.Com)而f（4）= ∴当k≥4时ak－bk≥………………10分

    又f（1）=f（2）=f（3）=0   ∴不存在k， 使f（k）∈（0，）…………12分

    20、证（Ⅰ）因为侧面，故

     在中，   由余弦定理有

    学科网(Zxxk.Com)  故有 

      而     且平面

          ………………  4分

    （Ⅱ）由

    从而  且 故

     不妨设  ，则，则

    又  则

    在中有   从而（舍去）

    故为的中点时，………………  8分

     法二：以为原点为轴，设，则

      由得   

     即  

    化简整理得       或

    当时与重合不满足题意

    当时为的中点

    故为的中点使………………  8分

     （Ⅲ）取的中点，的中点，的中点，的中点

     连则，连则，连则

     连则，且为矩形，

    又   故为所求二面角的平面角………………  10分

    学科网(Zxxk.Com)在中，

    ………………  12分

    法二：由已知， 所以二面角的平面角的大小为向量与的夹角………………  10分

    因为  

    故 ………………  12分

    21.解：（I）由，  ∴直线l的斜率为，

    故l的方程为，∴点A坐标为（1，0）……… 2分

    设    则，

    由得

    整理，得……………………4分

    ∴动点M的轨迹C为以原点为中心，焦点在x轴上，长轴长为，短轴长为2的椭圆 …… 5分

    （II）如图，由题意知直线l的斜率存在且不为零，设l方程为y=k（x－2）（k≠0）①

    高考资源网

    ，

    由△>0得0<k2<.  ………………  6分

     

    设E（x1，y1），F（x2，y2）,则 ②……………………………7分

    令，

    由此可得………………  8分

    由②知

    学科网(Zxxk.Com)

     

     

     

     

     

     

     

     

    .

    ∴△OBE与△OBF面积之比的取值范围是（3－2，1）.…………12分

    22解：（1）由题意知，的定义域为，

       …… 2分

    当时， ，函数在定义域上单调递增． … 3分

    （2） ①由（Ⅰ）得，当时，,函数无极值点．………………  5分                

    ②当时，有两个不同解，                       

    时，，,

    此时 ，随在定义域上的变化情况如下表：

    减

    极小值

    增

    由此表可知：时，有惟一极小值点，   …… 7分

    ii）   当时，0<<1    此时，，随的变化情况如下表：

     

    增

    极大值

    减

    极小值

    增

    由此表可知：时，有一个极大值和一个极小值点；…9分

    综上所述：当时，有惟一最小值点；

    当时，有一个极大值点和一个极小值点

    …….10分

    （3）由（2）可知当时，函数，此时有惟一极小值点

    且      …… 9分

                       …… 11分

    令函数       …… 12分

    …14分

     


    同步练习册答案