题目列表(包括答案和解析)
设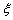
为随机变量，从棱长为1的正方体ABCD?A1B1C1D1的八个顶点中任取四个点，当四点共面时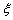，=0，当四点不共面时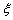，的值为四点组成的四面体的体积．
（1）求概率P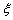（=0）；
（2）求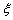的分布列，并求其数学期望E ()．
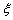设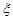
为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，
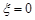；当两条棱平行时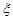，的值为两条棱之间的距离；当两条棱异面时，
．
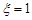（1）求概率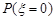
；
（2）求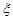的分布列，并求其数学期望
．
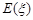设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ＝0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ＝1.
(1)求概率P(ξ＝0)；
(2)求ξ的分布列，并求其数学期望E(ξ)．
设
为随机变量，从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点，当四点共面时，=0，当四点不共面时，的值为四点组成的四面体的体积．
（1）求概率P（=0）；
（2）求的分布列，并求其数学期望E ()．
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
C
D
A
D
C
A
B
A
D
B
二、填空题
13．3 14．1 15．36π 16．
三、解答题
17．解：（1）
=
………………………….2分
=
.………………………………………4分
|
为偶函数，只需
…………………………………………….8分
，
.…………………………………………………………10分
,
,…………….2分
, 
，
.…………………………. …………4分
点作
于
,由正三棱柱性质知
平面
,
,则
在平面
，
，…………………………2分
中点，又
,
的中点.
于
,
,则
,
为二面角
的平面角.…4分
中，
=
，
，
.
..…6分
到平面
距离等于
平面
，
平面
于
，则
平面
.
.…………………………12分
，因为
，
时，
；当
时，
.
；
.………6分
得：
，
，则
，
时，
，
时，
，
在
上递减，在
上递增，…………………………10分
上只有一个实数根，则必须且只需
的取值范围
．……………………12分
，
，
.……………………………1分
，…2分
，
.……………………………………4分
………………………………6分
，得
，显然直线
，
的斜率都存在且都不为0.
，则
.
得
，同理可得
.………8分
则
.（当且仅当
时取等号）
的最小值是8.…………………………………………………………12分
，由数列
的递推公式得
，
，
.……………………………………………………3分
=
.……………………5分
为公差是
，得
.……………………7分
，
.……………………8分
=
，……………………10分
=
.……………………12分