
题目列表(包括答案和解析)
如图,已知正三棱柱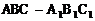 的各条棱长都为a,P为
的各条棱长都为a,P为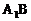 上的点。(1)试确定
上的点。(1)试确定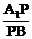 的值,使得PC⊥AB;
的值,使得PC⊥AB;
(2)若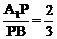 ,求二面角P—AC—B的大小;
,求二面角P—AC—B的大小;
(3)在(2)的条件下,求 到平面PAC的距离。
到平面PAC的距离。
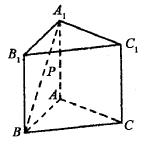
 的各条棱长都为a,P为
的各条棱长都为a,P为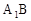 上的点。
上的点。 的值,使得PC⊥AB;
的值,使得PC⊥AB;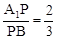 ,求二面角P—AC—B的大小;
,求二面角P—AC—B的大小;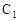 到平面PAC的距离。
到平面PAC的距离。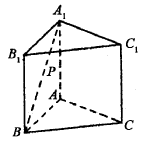
如图所示,已知正三棱柱![]() 的各条棱长都为
的各条棱长都为![]() ,P为
,P为![]() 上的点。
上的点。
(1)试确定![]() 的值,使PC
的值,使PC![]() AB;
AB;
(2)若![]() ,求二面角
,求二面角![]() 的大小;
的大小;
(3)在(2)的条件下,求![]() 到平面PAC的距离。
到平面PAC的距离。
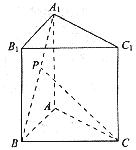
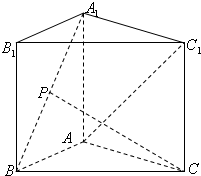 已知正三棱柱ABC-A1B1C1的各条棱长都相等,P为A1B上的点,
已知正三棱柱ABC-A1B1C1的各条棱长都相等,P为A1B上的点,| A1P |
| A1B |
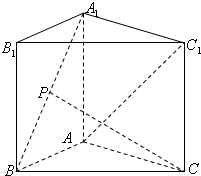 已知正三棱柱ABC-A1B1C1的各条棱长都相等,P为A1B上的点,
已知正三棱柱ABC-A1B1C1的各条棱长都相等,P为A1B上的点,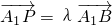 ,且PC⊥AB.
,且PC⊥AB.
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
C
D
A
D
C
A
B
A
D
B
二、填空题
13.3 14.1 15.36π 16..files/image211.gif)
三、解答题
17.解:(1).files/image213.gif)
.files/image215.gif)
=.files/image217.gif) ………………………….2分
………………………….2分
=.files/image219.gif) .………………………………………4分
.………………………………………4分
|