20090327 (2)要使函数.files/image225.gif) 为偶函数,只需 为偶函数,只需 .files/image227.gif)
即.files/image229.gif) …………………………………………….8分 …………………………………………….8分 因为.files/image140.gif) , , 所以.files/image232.gif) .…………………………………………………………10分 .…………………………………………………………10分 18.(1)由题意知随机变量ξ的取值为2,3,4,5,6. .files/image234.gif) , ,.files/image236.gif) ,…………….2分 ,…………….2分
.files/image238.gif) , , .files/image240.gif) , ,
.files/image242.gif) .…………………………. …………4分 .…………………………. …………4分
所以随机变量ξ的分布列为 .files/image142.gif)
2 3 4 5 6 P .files/image245.gif)
.files/image247.gif)
.files/image249.gif)
.files/image251.gif)
.files/image253.gif)
…………………………………………6分 (2)随机变量ξ的期望为.files/image255.gif) …………………………12分 19.解:(1)过.files/image149.gif) 点作 点作.files/image258.gif) 于 于.files/image260.gif) ,由正三棱柱性质知 ,由正三棱柱性质知.files/image262.gif) 平面 平面.files/image264.gif) , , 连接.files/image266.gif) ,则 ,则.files/image266.gif) 为 为.files/image268.gif) 在平面 在平面.files/image264.gif) 上的射影. 上的射影. .files/image270.gif) .files/image153.gif) , ,.files/image273.gif) .files/image275.gif) ,…………………………2分 ,…………………………2分
.files/image276.gif) .files/image273.gif) .files/image260.gif) 为 为.files/image280.gif) 中点,又 中点,又.files/image282.gif) , ,
所以.files/image149.gif) 为 为.files/image151.gif) 的中点. 的中点. 过.files/image260.gif) 作 作.files/image286.gif) 于 于.files/image288.gif) , , 连结.files/image290.gif) ,则 ,则.files/image292.gif) , , .files/image273.gif) .files/image295.gif) .files/image297.gif) 为二面角 为二面角
.files/image155.gif) 的平面角.…4分 的平面角.…4分
在.files/image300.gif) 中, 中, 由.files/image302.gif) = =.files/image304.gif) , ,.files/image306.gif) , , 得.files/image308.gif) . . 所以二面角.files/image155.gif) 的正切值为 的正切值为.files/image310.gif) ..…6分 ..…6分 (2).files/image270.gif) .files/image260.gif) 是 是.files/image280.gif) 中点, 中点, .files/image273.gif) .files/image057.gif) 到平面 到平面.files/image160.gif) 距离等于 距离等于.files/image260.gif) 到平面 到平面.files/image160.gif) 距离的2倍, 距离的2倍,
又由(I)知.files/image318.gif) 平面 平面.files/image320.gif) , , .files/image273.gif) 平面 平面.files/image320.gif) .files/image324.gif) 平面 平面.files/image160.gif) , ,
过.files/image260.gif) 作 作.files/image327.gif) 于 于.files/image329.gif) ,则 ,则.files/image331.gif) 平面 平面.files/image160.gif) , , .files/image334.gif) . .
故所求点.files/image057.gif) 到平面 到平面.files/image160.gif) 距离为 距离为.files/image337.gif) .…………………………12分 .…………………………12分 20.解:(1)函数.files/image225.gif) 的定义域为 的定义域为.files/image340.gif) ,因为 ,因为 .files/image342.gif) , ,
所以 当.files/image344.gif) 时, 时,.files/image346.gif) ;当 ;当.files/image348.gif) 时, 时,.files/image350.gif) . . 故.files/image225.gif) 的单调递增区间是 的单调递增区间是.files/image352.gif) ; ;.files/image225.gif) 的单调递减区间是 的单调递减区间是.files/image354.gif) .………6分 .………6分 (注: -1处写成“闭的”亦可) (2)由.files/image356.gif) 得: 得:.files/image358.gif) , , 令.files/image360.gif) ,则 ,则.files/image362.gif) , , 所以.files/image364.gif) 时, 时,.files/image366.gif) , ,.files/image368.gif) 时, 时,.files/image370.gif) , , 故.files/image372.gif) 在 在.files/image374.gif) 上递减,在 上递减,在.files/image376.gif) 上递增,…………………………10分 上递增,…………………………10分 要使方程.files/image356.gif) 在区间 在区间.files/image379.gif) 上只有一个实数根,则必须且只需 上只有一个实数根,则必须且只需 .files/image381.gif)
解之得.files/image383.gif) 所以实数.files/image059.gif) 的取值范围 的取值范围.files/image386.gif) .……………………12分 .……………………12分 21.解:(1)设.files/image388.gif) , , 因为抛物线的焦点.files/image390.gif) , , 则.files/image392.gif) .……………………………1分 .……………………………1分 .files/image394.gif) ,…2分 ,…2分
.files/image396.gif) , ,
而点A在抛物线上, .files/image398.gif) .……………………………………4分 .……………………………………4分
又.files/image400.gif) ………………………………6分 ………………………………6分 (2)由.files/image402.gif) ,得 ,得.files/image404.gif) ,显然直线 ,显然直线.files/image406.gif) , ,.files/image408.gif) 的斜率都存在且都不为0. 的斜率都存在且都不为0. 设.files/image406.gif) 的方程为 的方程为.files/image410.gif) ,则 ,则.files/image408.gif) 的方程为 的方程为.files/image412.gif) . . 由 .files/image414.gif) 得 得.files/image416.gif) ,同理可得 ,同理可得.files/image418.gif) .………8分 .………8分 .files/image420.gif) 则 则.files/image422.gif)
=.files/image424.gif) .files/image426.gif) .(当且仅当 .(当且仅当.files/image428.gif) 时取等号) 时取等号) 所以.files/image190.gif) 的最小值是8.…………………………………………………………12分 的最小值是8.…………………………………………………………12分 22.解:(1).files/image431.gif) ,由数列 ,由数列.files/image192.gif) 的递推公式得 的递推公式得 .files/image434.gif) , ,.files/image436.gif) , ,.files/image438.gif) .……………………………………………………3分 .……………………………………………………3分
(2).files/image440.gif) =.files/image442.gif) =.files/image444.gif) = =.files/image446.gif) .……………………5分 .……………………5分 .files/image273.gif) 数列 数列.files/image199.gif) 为公差是 为公差是.files/image446.gif) 的等差数列. 的等差数列.
由题意,令.files/image450.gif) ,得 ,得.files/image452.gif) .……………………7分 .……………………7分 (3)由(2)知.files/image454.gif) , , 所以.files/image456.gif) .……………………8分 .……………………8分 此时.files/image458.gif) = =.files/image460.gif) =.files/image462.gif) ,……………………10分 ,……………………10分 .files/image273.gif) .files/image465.gif) .files/image467.gif)
.files/image273.gif) .files/image469.gif)
.files/image471.gif) = =.files/image473.gif)
.files/image475.gif)
>.files/image477.gif) .……………………12分 .……………………12分
| |

 中,
中,  ;
; 的正切值.
的正切值.
![]() 中,
中,![]()
![]() ;
; ![]() 的正切值。
的正切值。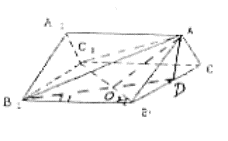
![]() ;
; ![]() 的正切值。
的正切值。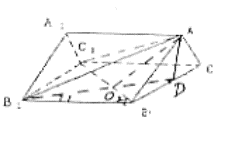
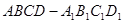 中.
中. 与
与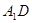 所成角的大小;
所成角的大小; 的正切值.
的正切值.
 中.
中.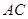 与
与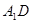 所成角的大小;
所成角的大小;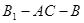 的正切值.
的正切值.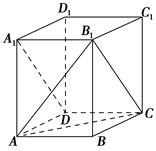
.files/image211.gif)
.files/image213.gif)
.files/image215.gif)
.files/image217.gif) ………………………….2分
………………………….2分.files/image219.gif) .………………………………………4分
.………………………………………4分