练习册

  • 练习册
  • 试题
    (1)求导数(x), 【查看更多】

     

    题目列表(包括答案和解析)

    （1）求f(x)=
    lnx+2x
    x2
    的导数；
    （2）求过曲线y=cosx上点P(
    π
    3
    ，
    1
    2
    )    且与过这点的切线垂直的直线方程．

    查看答案和解析>>

    设f（x）是定义在（0，+∞）上的单调可导函数．已知对于任意正数x，都有f[f(x)+
    2
    x
    ]=
    1
    f(x)
    ，且f（1）=a＞0．
    （Ⅰ）求f（a+2），并求a的值；
    （Ⅱ）令an=
    1
    f(n)
    ，n∈N*    ，证明：数列{an}是等差数列．

    查看答案和解析>>

    （1）求y=x(x2+
    1
    x
    +
    1
    x3
    )    的导数；
    （2）求y=(
    		x
    +1)(
    1
    		x
    -1)    的导数；
    （3）求y=x-sin
    x
    2
    cos
    x
    2
    的导数；
    （4）求y=
    x2
    sinx
    的导数；
    （5）求y=
    3x2-x
    		x
    +5
    		x
    -9
    		x
    的导数分

    查看答案和解析>>

    设f（x）是定义在区间（1，+∞）上的函数，其导函数为f′（x）．如果存在实数a和函数h（x），其中h（x）对任意的x∈（1，+∞）都有h（x）＞0，使得f′（x）=h（x）（x2-ax+1），则称函数f（x）具有性质P（a），设函数f（x）=lnx+
    b+2x+1
    (x＞1)    ，其中b为实数．
    （1）①求证：函数f（x）具有性质P（b）；
    ②求函数f（x）的单调区间．
    （2）已知函数g（x）具有性质P（2），给定x1，x2∈（1，+∞），x1＜x2，设m为实数，α=mx1+（1-m）x2，β=（1-m）x1+mx2，α＞1，β＞1，若|g（α）-g（β）|＜|g（x1）-g（x2）|，求m的取值范围．

    查看答案和解析>>

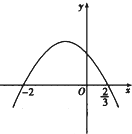    精英家教网设f（x）=ax3+bx2+cx的极小值为-8，其导函数y=f′（x）的图象经过点(-2，0)，(
    23
    ，0)    ，如图所示，
    （1）求f（x）的解析式；
    （2）若对x∈[-3，3]都有f（x）≥m2-14m恒成立，求实数m的取值范围．

    查看答案和解析>>

     

    一、选择题

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    答案

    A

    B

    A

    B

    C

    D

    A

    D

    C

    A

    B

    D

     

    二、填空题

    13. 165    14. 3   15. 36π    16. 6ec8aac122bd4f6e

    三、解答题

    17. 解：（1）6ec8aac122bd4f6e6ec8aac122bd4f6e

    =6ec8aac122bd4f6e………………………….2分

    =6ec8aac122bd4f6e.………………………………………4分

    20090327

    （2）要使函数6ec8aac122bd4f6e为偶函数，只需

       6ec8aac122bd4f6e 即6ec8aac122bd4f6e………….8分

       因为6ec8aac122bd4f6e，

       所以6ec8aac122bd4f6e.………………………………………………………10分

    18．解：（1）6ec8aac122bd4f6e.………………………….4分

    （2）由题意知n的取值为2，3，4，5,6.

    6ec8aac122bd4f6e，  6ec8aac122bd4f6e，

    6ec8aac122bd4f6e，

    6ec8aac122bd4f6e.    …10分

    所以6ec8aac122bd4f6e等于5时6ec8aac122bd4f6e最大，最大值为     

    6ec8aac122bd4f6e.…. …………12分 

    19．解：（Ⅰ）过6ec8aac122bd4f6e点作6ec8aac122bd4f6e于6ec8aac122bd4f6e,由正三棱柱性质知，

    6ec8aac122bd4f6e平面6ec8aac122bd4f6e,………2分

    连接6ec8aac122bd4f6e,则6ec8aac122bd4f6e为6ec8aac122bd4f6e在平面6ec8aac122bd4f6e上的射影.

    6ec8aac122bd4f6e   6ec8aac122bd4f6e，

    6ec8aac122bd4f6e6ec8aac122bd4f6e，……………4分

    6ec8aac122bd4f6e6ec8aac122bd4f6e为6ec8aac122bd4f6e中点，又6ec8aac122bd4f6e,所以6ec8aac122bd4f6e为6ec8aac122bd4f6e的中点即6ec8aac122bd4f6e.………………6分

    （2）过6ec8aac122bd4f6e作6ec8aac122bd4f6e于6ec8aac122bd4f6e,连结6ec8aac122bd4f6e,则6ec8aac122bd4f6e,

    6ec8aac122bd4f6e6ec8aac122bd4f6e6ec8aac122bd4f6e为二面角

    6ec8aac122bd4f6e6ec8aac122bd4f6e的平面角. ………………9分

    在6ec8aac122bd4f6e中，由6ec8aac122bd4f6e=6ec8aac122bd4f6e，

    6ec8aac122bd4f6e，得

    6ec8aac122bd4f6e.

    所以二面角6ec8aac122bd4f6e的

    平面角的正切值为6ec8aac122bd4f6e.…………12分

    20．解：（1）由6ec8aac122bd4f6e得

        6ec8aac122bd4f6e………………………….2分

    即6ec8aac122bd4f6e………………………….………………………….3分

    所以数列6ec8aac122bd4f6e是首项为6ec8aac122bd4f6e，公比为2的等比数列.

    所以数列6ec8aac122bd4f6e的通项公式6ec8aac122bd4f6e.………………………………6分

    （2）由6ec8aac122bd4f6e，得6ec8aac122bd4f6e..………………… 8分

    所以6ec8aac122bd4f6e=6ec8aac122bd4f6e

              =6ec8aac122bd4f6e…………..………………………………12分

    21．解：（1）6ec8aac122bd4f6e.……………………………2分

    （2）由6ec8aac122bd4f6e，

    由6ec8aac122bd4f6e得6ec8aac122bd4f6e或x=6ec8aac122bd4f6e，.……………………………4分

    又6ec8aac122bd4f6e

    6ec8aac122bd4f6e在[-2，2]上最大值6ec8aac122bd4f6e，最小值6ec8aac122bd4f6e..……………………………8分

    （3）6ec8aac122bd4f6e， 由题意知

    6ec8aac122bd4f6e...……………………12分

    22．解：（Ⅰ）设6ec8aac122bd4f6e，

    因为抛物线的焦点6ec8aac122bd4f6e，

    则6ec8aac122bd4f6e.……………………………1分

    6ec8aac122bd4f6e，………2分

    6ec8aac122bd4f6e，而点A在抛物线上，

    6ec8aac122bd4f6e.……………………………………4分

    又6ec8aac122bd4f6e故所求抛物线的方程为6ec8aac122bd4f6e.6分

    （2）由6ec8aac122bd4f6e，得6ec8aac122bd4f6e，显然直线6ec8aac122bd4f6e，6ec8aac122bd4f6e的斜率都存在且都不为0.

    设6ec8aac122bd4f6e的方程为6ec8aac122bd4f6e，则6ec8aac122bd4f6e的方程为6ec8aac122bd4f6e.

        由 6ec8aac122bd4f6e得6ec8aac122bd4f6e，同理可得6ec8aac122bd4f6e.……………8分

    则6ec8aac122bd4f6e

    =6ec8aac122bd4f6e6ec8aac122bd4f6e.（当且仅当6ec8aac122bd4f6e时取等号）

    所以6ec8aac122bd4f6e的最小值是8.……………………………………12分

     


    同步练习册答案