
题目列表(包括答案和解析)
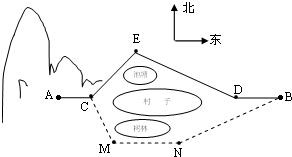 某村子的正西是一片山区.山脚下A处已建一处采石场,村子的北边有一池塘,南边有一树林,在B处是个石粉厂,在采石场采到的石料由公路ACEDB运输到石粉厂,如图所示.已知A,C,D,B在一条直线上,AC=2km,CE=2km,ED=3km,DB=2km,∠CED=120°.
某村子的正西是一片山区.山脚下A处已建一处采石场,村子的北边有一池塘,南边有一树林,在B处是个石粉厂,在采石场采到的石料由公路ACEDB运输到石粉厂,如图所示.已知A,C,D,B在一条直线上,AC=2km,CE=2km,ED=3km,DB=2km,∠CED=120°. 如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+
如图,成都市准备在南湖的一侧修建一条直路EF,另一侧修建一条观光大道,大道的前一部分为曲线段FBC,该曲线段是函数y=Asin(ωx+| 2π | 3 |
 (2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(1≤t≤
(2012•盐城一模)在综合实践活动中,因制作一个工艺品的需要,某小组设计了如图所示的一个门(该图为轴对称图形),其中矩形ABCD的三边AB、BC、CD由长6分米的材料弯折而成,BC边的长为2t分米(1≤t≤| 3 |
| 2 |
| 9 |
| 8 |
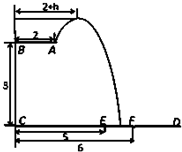 某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段,已知跳水板AB长为2m,跳水板距水面CD的高BC为3m,CE=5m,CF=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点hm(h≥1)到达距水面最大高度4m,规定:以CD为横轴,CB为纵轴建立坐标系.
某跳水运动员在一次跳水训练时的跳水曲线为如图所示的抛物线一段,已知跳水板AB长为2m,跳水板距水面CD的高BC为3m,CE=5m,CF=6m,为安全和空中姿态优美,训练时跳水曲线应在离起跳点hm(h≥1)到达距水面最大高度4m,规定:以CD为横轴,CB为纵轴建立坐标系.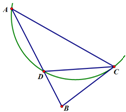 如图,
如图, |
| AC |
 |
| AC |
 |
| AC |
| 5 |
| 2 |
| 25 |
| 13 |
| 25 |
| 13 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com