练习册

  • 练习册
  • 试题
    设实数x, y满足.则的最小值为( ) 【查看更多】

     

    题目列表(包括答案和解析)

    设实数x，y满足约束条件 
    2x-y+2≥0
    8x-y-4≤0
    x≥0，y≥0
    ，若目标函数z=abx+y（a＞0，b＞0）的最大值为8，则
    1
    a2
    +
    1
    b2
    的最小值是
     
    ．

    查看答案和解析>>

    设实数x、y满足
    x≥0
    x-2y≥0
    x-y-2≤0
    ，则使z=-3x+4y取最小值的点为
    （0，-2）
    （0，-2）
    ．

    查看答案和解析>>

    设实数x，y满足条件：①x≥0，y≥0；②3x-y-6≤0；③x-y+2≥0，目标函数z=ax+by（a＞0，b＞0）的最大值为12，则
    2
    a
    +
    3
    b
    的最小值是
     
    ．

    查看答案和解析>>

    设实数x，y满足不等式组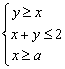．若z＝3x＋y的最大值是最小值的2倍，则a的值为　　　　　　　　　                        （　　）

    A.                     B. 3                  C.               D.2

    查看答案和解析>>

    设实数x，y满足，则x+2y的最小值为（    ）。

    查看答案和解析>>

                       高三数学试卷（文科）                 2009.4   

    题号

    1

    2

    3

    4

    5

    6

    7

    8

    答案

    C

    B

    A

    B

    A

    D

    C

    A

    一、选择题：本大题共 8 小题，每小题 5 分，共 40 分.

     

     

     

    二、填空题：本大题共 6 小题，每小题 5 分，共 30 分.

    9. 36         10. 10        11. 2, 8      12.      13.        14. 5, 2     

    注：两空的题目，第一个空3分，第二个空2分.

    三、解答题：本大题共 6 小题，共 80 分.

    15.（本小题满分12分）

    （Ⅰ）解：由余弦定理，                       ----------------------------3分

    得.                                 ---------------------------5分

    （Ⅱ）解：由（Ⅰ）知 ,

    所以角为锐角，所以，          ----------------------------7分

    则     --------------------------10分

                              

       .

            所以.                             ---------------------------12分

    16.（本小题满分12分）

    （Ⅰ）解：记 “2次汇报活动都是由小组成员甲发言” 为事件A.   -----------------------------1分     

    由题意，得事件A的概率，              

    即2次汇报活动都是由小组成员甲发言的概率为.            ---------------------------5分

    （Ⅱ）解：由题意，每次汇报时，男生被选为代表的概率为，女生被选为代表的概率为.

                                                                   ----------------------------6分

          记“男生发言次数不少于女生发言次数”为事件B，

    由题意，事件B包括以下两个互斥事件：

    1事件B1：男生发言2次女生发言0次，其概率为

    ，             ----------------------------8分

    2事件B2：男生发言1次女生发言1次，其概率为

    ，           ----------------------------10分

    所以，男生发言次数不少于女生发言次数的概率为.

       ---------------------------12分

    17.（本小题满分14分）

    方法一：（Ⅰ）证明：在中，，

           ，

           ，即，                             ---------------------------1分

           ，

           平面.                                      ---------------------------4分

    （Ⅱ）如图，连接AC，由（Ⅰ）知平面，

         AC为PA在平面ABCD内的射影，

         为PA与平面ABCD所成的角.    --------------6分

         在中，，，

         ，

        在中，，，

        ，

        PA与平面ABCD所成角的大小为.                ---------------------------8分

    （Ⅲ）由（Ⅰ）知，

    又，

    平面.                                       ---------------------------9分

    如图，过C作于M，连接BM，

    是BM在平面PCD内的射影，

    ，

    为二面角B-PD-C的平面角.                       ---------------------------11分

    在中, , PC=1, ，

    ，

    又，，

    ，

    在中, , BC=1, ,

    ,

    二面角B-PD-C的大小为.                       --------------------------14分

      方法二：（Ⅰ）同方法一.                                        ---------------------------4分

       （Ⅱ）解：连接AC，由（Ⅰ）知平面，

         AC为PA在平面ABCD内的射影，

           为PA与平面ABCD所成的角.                     ---------------------------6分

           如图，在平面ABCD内，以C为原点， CD、CB、CP分别为x、y、z轴，建立空间直角坐标系C-xyz，

             则, ，                    

                                                                     ---------------------------7分

           ，

           PA与平面ABCD所成角的大小为.               ---------------------------9分

     （Ⅲ）过C作于M，连接BM，设，

           则，

    ，

    ；           1       

    共线，

    ，               2

    由12，解得，

    点的坐标为，，，

    ,

    ，

    又，

    为二面角B-PD-C的平面角.                       ---------------------------12分

             ，，

             ， 

     二面角B-PD-C的大小为.                        --------------------------14分

    18.（本小题满分14分）

    （Ⅰ）解：因为，

          所以当时，，解得，           ---------------------------2分

              当时，，即，解得，

          所以，解得；                                 ---------------------------5分

    则，数列的公差，

    所以.                            ---------------------------8分

    （Ⅱ）因为

                         ---------------------------9分

            ---------------------------12分

    .                       

    因为，

    所以 .                          -------------------------14分

            注：为降低难度，此题故意给出多余条件，有多种解法，请相应评分.

    19.（本小题满分14分）

       （Ⅰ）解：设A(x1, y1)，

    因为P为AM的中点，且P的纵坐标为0，M的纵坐标为1，

    所以，解得，                              -------------------------1分

    又因为点A(x1, y1)在椭圆C上，

    所以，即，解得，

     则点A的坐标为或，                      -------------------------3分

    所以直线l的方程为，或.    -------------------------5分

       （Ⅱ）设A(x1, y1)，B(x2, y2)，则

    所以，

             则，                   -------------------------7分

             当直线AB的斜率不存在时，其方程为，，此时；

    -------------------------8分

    当直线AB的斜率存在时，设其方程为，

       由题设可得A、B的坐标是方程组的解，

       消去y得，

       所以，       -------------------------10分

       则，

       所以，

       当时，等号成立, 即此时取得最大值1.    -------------------------13分

    综上，当直线AB的方程为或时，有最大值1.  -------------------14分

    20.（本小题满分14分）

    （Ⅰ）解：当时，，

    因为，

    所以，函数的图象不能总在直线的下方.          ---------------------------3分

    （Ⅱ）解：由题意，得，

    令，解得或，                     --------------------------4分

    当时，由，解得，

    所以在上是增函数，与题意不符，舍去；

    当时，由，与题意不符，舍去；     --------------------------6分

    当时，由，解得，

    所以在上是增函数，

    又在(0，2)上是增函数，

                  所以，解得，

    综上，a的取值范围为.                            ---------------------------9分

    （Ⅲ）解：因为方程最多只有3个根，

          由题意，得在区间内仅有一根，

          所以，           1

    同理，           2       --------------------------11分

    当时，由1得 ，即，

        由2得，即，

        因为，所以，即；

    当时，由1得 ，即，

        由2得，即，

        因为，所以，即；

    当时，因为，所以有一根0，这与题意不符.

    综上，.                                          ---------------------------14分

    注：在第（Ⅲ）问中，得到12后，可以在坐标平面aOb内，用线性规划方法解. 请相应评分.

           

         

     

     


    同步练习册答案