
题目列表(包括答案和解析)
已知 ,
, ,规定:当
,规定:当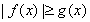 时,
时, 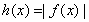 ;当
;当 时,
时, ,则
,则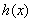 ( )
( )
A.有最小值 ,最大值1 B.有最大值1,无最小值
,最大值1 B.有最大值1,无最小值
C.有最小值 ,无最大值 D.有最大值
,无最大值 D.有最大值 ,无最小值
,无最小值
已知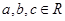 ,给出下列命题:
,给出下列命题:
①若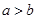 ,则
,则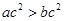 ;②若ab≠0,则
;②若ab≠0,则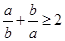 ;③若
;③若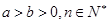 ,则
,则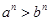 ;
;
④若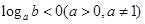 ,则a,b中至少有一个大于1.其中真命题的个数为( )
,则a,b中至少有一个大于1.其中真命题的个数为( )
(A)2 (B)3 (C)4 (D)1
已知 ,
,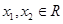 ,则有:( )
,则有:( )
A.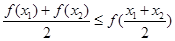 B.
B.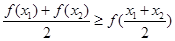
C. D.以上都不是
D.以上都不是
已知 ,并设:
,并设:

 ,
, 至少有3个实根;
至少有3个实根;
 当
当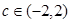 时,方程
时,方程 有9个实根;
有9个实根;
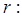 当
当 时,方程
时,方程 有5个实根。
有5个实根。
则下列命题为真命题的是( )
A. B.
B.  C. 仅有
C. 仅有 D.
D. 
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
C
A
C
B
A
D
D
A/B
B
D
二、 填空题:
13. 8
14.(理) (文)
(文)
15. 
16. 或
或  或
或 
三、解答题: 答案仅供参考,其他解法参照给分
17.(本小题满分12分)
(理) 解:

(文) 解:(1)由两角和差公式及二倍角公式得

由 得
得

于是函数 的单调递增区间为
的单调递增区间为 -------------6分
-------------6分
(2)由(1)知
再由 得------------------------8分
得------------------------8分
 --------------------10分
--------------------10分
所以函数 的值域为
的值域为 -------------------------12分
-------------------------12分
18.(本小题满分12分)
(理) 解:(1)该考生得50分的情况有三类;①在“两道只能分别判断2个选项是错误的”时,该两题竟然全选对后面两道题全选错,其概率为 ;②在“两道只能分别判断2个选项是错误的”时,该两题竟然全选错后面两道题全选对,其概率为
;②在“两道只能分别判断2个选项是错误的”时,该两题竟然全选错后面两道题全选对,其概率为 ;③在“两道只能分别判断2个选项是错误的”时,该两题只能选对一道后面两道题也只能一错一对,其概率为
;③在“两道只能分别判断2个选项是错误的”时,该两题只能选对一道后面两道题也只能一错一对,其概率为 ,从而有
,从而有
 …………………………………4分
…………………………………4分
(2)用 表示所得分数,则
表示所得分数,则 可能的取值为40,45,50,55,60
可能的取值为40,45,50,55,60
∵



 ……………8分
……………8分
∴ 的概率分布列为
的概率分布列为

40
45
50
55
60
P





 …12分
…12分
(文) 解: (I)记“取到的4个球全是红球”为事件A,则

 ……………………… 4分
……………………… 4分
(II)记“取到的4个球至多有1个红球”为事件B,“取到的4个球只有1个红球”为事件

 由题意得
由题意得
 ………………………6分
………………………6分

 ………………………8分
………………………8分

 ………………………10分
………………………10分
所以,

化简,得
解得
n=2,或 故n=2. ………………………12分
故n=2. ………………………12分
19.(本小题满分12分)
证明: (I)连结PA.
∵ PD⊥平面ABCD, CD⊥AD,
∴ PA⊥CD(三垂线定理).………………2分
∵ M、N分别是PB、AB的中点,
∴ MN∥PA,
∴ MN⊥CD.………………………6分
(理)(II) 过点O作DN的垂线OE,垂足为E,连结ME.
∵ MO⊥平面ABCD,∴ ME⊥DN.
∴ ∠MEO就是二面角M-DN-C的平面角. ………………………9分
∵ △MOE中,∠MOE=90°,MO=3,OE= ,
,
∴  .
.
故二面角M-DN-C的大小为 .………………………12分
.………………………12分
(文)(II)设AC、BD交于点O.
∵ MO∥PD,
∴ MO⊥底面ABCD,且MO= PD=3.
PD=3.
………………………9分
∵ N是AB的中点,
∴  , ∴
, ∴ ,
,
∴  ………………………12分
………………………12分
20.(本小题满分12分)
(理) 解:(1)令 ,
,
则 ,---------------------------------------2分
,---------------------------------------2分
由 得,
得,
由 得,
得, ---------------------------------4分
---------------------------------4分
由 的定义域
的定义域 知,
知,
 的单调递增区间为
的单调递增区间为 ;递减区间为
;递减区间为 --------------------6分
--------------------6分
(2) 令 ,则函数
,则函数 与
与 的图象有且只有两个不同的交点
的图象有且只有两个不同的交点 与x轴正半轴有且只有两个不同的交点.对
与x轴正半轴有且只有两个不同的交点.对 求导数,得----------8分
求导数,得----------8分

 .
.
又∵x→0时, <0,x→+∞时,
<0,x→+∞时, >0------------------------------------------10分
>0------------------------------------------10分
 有两个不同正根的充要条件是
有两个不同正根的充要条件是 或
或
 ,解得m=7或m=
,解得m=7或m= .---------------------------12分
.---------------------------12分
也可由(1)知,函数 在
在 处取得极值,若要恰有两不同的根,则必有
处取得极值,若要恰有两不同的根,则必有 或
或 ,所以有m=7或m=
,所以有m=7或m=
(文)解:(Ⅰ)
 ,
,
 ---------------2分
---------------2分
 -----------------------------------4分
-----------------------------------4分
又
故所求 。----------------------6分
。----------------------6分
(Ⅱ)由(Ⅰ)知

由 得,
得, ,
,
由 得,
得,  ,
,
故函数 的单调递增区间为
的单调递增区间为 单调递减区间为
单调递减区间为 ------8分
------8分

 恒成立,
恒成立,
故函数 在单调递增区间为
在单调递增区间为 ---------------10分
---------------10分

由 得,
得, ,
,
由 得,
得,  ,
,
故函数 的单调递增区间为
的单调递增区间为 单调递减区间为
单调递减区间为 ----12分
----12分
21.(本小题满分12分)
(理)解:(1)由已知设椭圆方程为 ,
,
则 ---------------2分
---------------2分
 a=2, c=
a=2, c= ,
,  b=1.---------------------------------4分
b=1.---------------------------------4分
∴椭圆的标准方程为 ----------------------------------------------6分
----------------------------------------------6分
(2)当直线BC垂直于x轴时,BC=2,因此△ABC的面积S△ABC=1.
当直线BC不垂直于x轴时,说该直线方程为y=kx,代入 ,
,
解得B( ,
, ),C(-
),C(- ,-
,- ),------------8分
),------------8分
则 ,又点A到直线BC的距离d=
,又点A到直线BC的距离d= ,
,
∴△ABC的面积S△ABC=
于是S△ABC= ----------------------------10分
----------------------------10分
由 ≥-1,得S△ABC≤
≥-1,得S△ABC≤ ,其中,当k=-
,其中,当k=- 时,等号成立.
时,等号成立.
∴S△ABC的最大值是 .
-------------------------------12分
.
-------------------------------12分
(文)解:(Ⅰ)设 ,由
,由 知,点C的轨迹为
知,点C的轨迹为 .
.
由 消y,得
消y,得  .
.
设 ,
, ,则
,则 ,
, .………………………4分
.………………………4分
所以, ,
,
所以  ,
,
于是  .………………………………………………………6分
.………………………………………………………6分
(Ⅱ)假设存在过点P的弦EF符合题意,则此弦的斜率不为零,设此弦所在直线的方程为 .
.
由 消x,得
消x,得 .
.
设 ,
, ,则
,则 ,
, .…………………8分
.…………………8分
因为过点P作抛物线的弦的长度是原点到弦的中点距离的2倍,所以  ,
,
即 , ……………………10分
, ……………………10分
所以  ,得
,得  .
.
所以,存在 .………………………………………………………12分
.………………………………………………………12分
22.(本小题满分14分)
(理 )解:(I) 由已知,得  ,
,
即 , ………………………2分
, ………………………2分
所以数列{ }是公比为2的等比数列,首项为
}是公比为2的等比数列,首项为 =2,
=2,
故 =
= . ………………………4分
. ………………………4分
也可以用累积法
(II) 因为 =
= ,
,
若 =
= 恒成立,则
恒成立,则 恒成立,所以
恒成立,所以
 ………………………6分
………………………6分
解出 A=1,B=-4,C=6.
故存在常数A,B,C满足条件. ………………………8分
(III) =(b2-b1)+(b3-b2)+(b4-b3)+…+(bn+1-bn)=bn+1-b1
=(b2-b1)+(b3-b2)+(b4-b3)+…+(bn+1-bn)=bn+1-b1
=
=  ………………………11分
………………………11分
< 
=
= 
= 
≤  .………………………14分
.………………………14分
别证:可以应用数学归纳法.
(文) 解:(Ⅰ) ,
, . ---------------4分
. ---------------4分
(Ⅱ)∵ ,且
,且 ∴
∴ .-------------------------------8分
.-------------------------------8分
(Ⅲ)设第 个图形的边数为
个图形的边数为
∴ ,且
,且 , ∴
, ∴ .
.
∵第 个图形的面积为
个图形的面积为 则
则 ------------------------10分
------------------------10分
= =
=
∴

……

 ------------------------------------------12分
------------------------------------------12分
上述 个式子两边分别相加得:
个式子两边分别相加得:
 ]
]
∴
∴ -------------------------------------------------------------------14分
-------------------------------------------------------------------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com