
题目列表(包括答案和解析)
求顶点在原点,焦点在![]() 轴上,且截直线
轴上,且截直线![]() 所得的弦长为
所得的弦长为![]() 的抛物线的方程。
的抛物线的方程。
求下列抛物线的方程
(1)顶点在原点,焦点在y轴上,抛物线上点(3,a)到焦点的距离是5;
(2)顶点在原点,焦点在x轴上的抛物线截直线![]() 所得的弦长为
所得的弦长为![]() 。
。
求与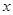 轴切于点(5,0)并在y轴上截取弦长为10的圆的方程。
轴切于点(5,0)并在y轴上截取弦长为10的圆的方程。
一、选择题:(本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中。只有一项是符合题目要求的。)
B、D、C、A B、A、D、B
二、填空题:(本大题共7小题,每小题5分,满分30分。其中13~15题是选做题,考生只能选做两题,三题全答的,只计算前两题得分。)
9、 ; 10、800; 11、①③④; 12、
; 10、800; 11、①③④; 12、 ,1005;
,1005;
13、 14、
14、 ; 15、
; 15、
三、解答题:(本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤。)
16、(1)证明:∵PA⊥底面ABCD,MN 底面ABCD
底面ABCD
∴MN⊥PA 又MN⊥AD 且PA∩AD = A
∴MN⊥平面PAD ………………………………………………4分
MN 平面PMN ∴平面PMN⊥平面PAD ……………………6分
平面PMN ∴平面PMN⊥平面PAD ……………………6分
(2)∵BC⊥BA BC⊥PA PA∩BA = A ∴BC⊥平面PBA
∴∠BPC为直线PC与平面PBA所成的角
即 ……………………………………………10分
……………………………………………10分
在 中,
中,
∴ ………………12分
………………12分
17、解:(1)由题意可知 、
、 、
、 、
、 、
、 这5个点相邻两点间的弧长为
这5个点相邻两点间的弧长为

 的可能的取值有
的可能的取值有 ,2
,2 ,3
,3 ,4
,4
 ,
,
 ,
,
于是 =
= ×
× +2
+2 ×
× +3
+3 ×
× +4
+4 ×
× =2
=2 。…………………6分
。…………………6分
(2)连结MP,取线段MP的中点D,则OD⊥MP,易求得OD= ,
,
当S点在线段MP上时,三角形SAB的面积等于 ×
× ×8 =
×8 = ,
,
 所以只有当S点落在阴影部分时,面积才能大于
所以只有当S点落在阴影部分时,面积才能大于 ,
,
S阴影
= S扇形OMP - S△OMP =  ×
× ×
× -
- ×
× = 4
= 4 -8,
-8,
所以由几何概型公式的三角形SAB的面积大于 的概
的概
率P = 。 …………………12分
。 …………………12分
18、解:(1)证明:在 中,由题设
中,由题设 ,AD = 2可得
,AD = 2可得
 ,于是
,于是 。在矩形
。在矩形 中,
中, .
.
又 ,所以
,所以 平面
平面 .…………………………………….4分
.…………………………………….4分
(2)解:由题设, ,所以
,所以 (或其补角)是异面直线
(或其补角)是异面直线 与
与 所成的角.
所成的角.
在 中,由余弦定理得
中,由余弦定理得
由(1)知 平面
平面 ,
, 平面
平面 ,
,
所以 ,因而
,因而 ,于是
,于是 是直角三角形,
是直角三角形,
故 ………………………….8分
………………………….8分
(3)解:过点P做 于H,过点H做
于H,过点H做 于E,连结PE
于E,连结PE

 平面
平面 ,
, 平面
平面 ,
,
 .又
.又 ,
,
因而 平面
平面 ,
, 平面
平面 ,
,
又 ,
, ,
,
 平面
平面 ,又
,又 平面
平面

 ,从而
,从而 是二面角
是二面角 的平面角…………….12分
的平面角…………….12分
 由题设可得,
由题设可得,

于是在 中,
中, ….14分
….14分
19、解: (1)依题意知,数列 是一个以500为首项,-20为公差的等差数列,所以
是一个以500为首项,-20为公差的等差数列,所以
则 时不等式①成立
…………………13分
时不等式①成立
…………………13分
答:从今年起该企业至少经过4年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润……………………………………………….……14分
20、(1)连接 ,
,  E、F分别为
E、F分别为 、DB的中点,
、DB的中点, EF//
EF// ,
,
又
 平面
平面 ,EF
,EF 平面
平面 ,
,
 EF//平面
EF//平面 ………………………………………………………4分
………………………………………………………4分
(2)正方体 中,
中, 平面
平面 ,
, 平面
平面
则
 ,正方形
,正方形 中,
中, ,
,
又 = B,AB、
= B,AB、 平面
平面 ,
,
则 平面
平面 ,
,
 平面
平面 ,所以
,所以
 ,又EF//
,又EF// ,
,
所以 EF. ……………………………………………………………9分
EF. ……………………………………………………………9分
(3) 正方体
正方体 的棱长为2,
的棱长为2, 、
、 分别为
分别为 、DB的中点。
、DB的中点。













 ……………………………..………………14分
……………………………..………………14分
21、解:(1) …………………………………2分
…………………………………2分
 在
在 上是增函数,
上是增函数, 在
在 上恒成立
上恒成立
即 …………………………………………4分
…………………………………………4分
 (当且仅当
(当且仅当 时取等号)
时取等号)
所以 ……………………..………………6分
……………………..………………6分
(2)设 ,则
,则
当 时,
时, 在区间
在区间 上是增函数
上是增函数
所以 的最小值为
的最小值为 ……………………………………………10分
……………………………………………10分
当 时,
时,
因为函数 在区间
在区间 上是增函数,在区间
上是增函数,在区间 上也是增函数,
上也是增函数,
又 在
在 上为连续函数,所以
上为连续函数,所以 在
在 上为增函数,
上为增函数,
所以 的最小值为
的最小值为
 ……………………………………14分
……………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com