
题目列表(包括答案和解析)
如图,三棱柱 中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。
中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点。

(I) 证明:平面 ⊥平面
⊥平面
(Ⅱ)平面 分此棱柱为两部分,求这两部分体积的比.
分此棱柱为两部分,求这两部分体积的比.
【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算,考查空间想象能力、逻辑推理能力,是简单题.
【解析】(Ⅰ)由题设知BC⊥ ,BC⊥AC,
,BC⊥AC, ,∴
,∴ 面
面 , 又∵
, 又∵
 面
面 ,∴
,∴ ,
,
由题设知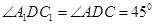 ,∴
,∴ =
= ,即
,即 ,
,
又∵ , ∴
, ∴ ⊥面
⊥面 , ∵
, ∵
 面
面 ,
,
∴面 ⊥面
⊥面 ;
;
(Ⅱ)设棱锥 的体积为
的体积为 ,
, =1,由题意得,
=1,由题意得, =
= =
= ,
,
由三棱柱 的体积
的体积 =1,
=1,
∴ =1:1, ∴平面
=1:1, ∴平面 分此棱柱为两部分体积之比为1:1
分此棱柱为两部分体积之比为1:1
 (2012•长宁区二模)棱锥的底面是正三角形,边长为1,棱锥的一条侧棱与底面垂直,其余两条侧棱与底面所成角都等于
(2012•长宁区二模)棱锥的底面是正三角形,边长为1,棱锥的一条侧棱与底面垂直,其余两条侧棱与底面所成角都等于| π | 3 |
如图,在正四棱锥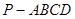 中,
中,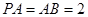 .
.
(1)求该正四棱锥的体积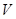 ;
;
(2)设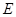 为侧棱
为侧棱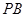 的中点,求异面直线
的中点,求异面直线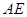 与
与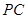
所成角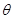 的大小.
的大小.
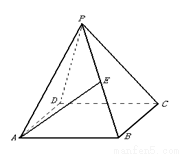
【解析】第一问利用设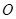 为底面正方形
为底面正方形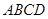 中心,则
中心,则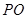 为该正四棱锥的高由已知,可求得
为该正四棱锥的高由已知,可求得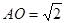 ,
,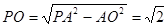
所以,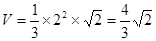
第二问设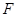 为
为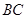 中点,连结
中点,连结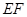 、
、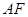 ,
,
可求得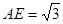 ,
,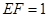 ,
,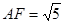 ,
,
在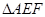 中,由余弦定理,得
中,由余弦定理,得
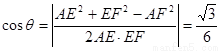 .
.
所以,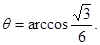
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com