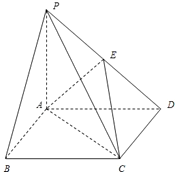如图，四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PB⊥BC，PD⊥CD，且PA=2，E为PD中点．
（Ⅰ）求证：PA⊥平面ABCD；
（Ⅱ）求二面角E-AC-D的大小；
（Ⅲ）在线段BC上是否存在点F，使得点E到平面PAF的距离为

2 5

5

？若存在，确定点F的位置；若不存在，请说明理由．

如图,正方体ABCD—A₁B₁C₁D₁的棱长为1,E为A₁B₁的中点,则下列四个命题:

①点E到平面ABC₁D₁的距离为;②直线BC与平面ABC₁D₁所成的角等于45°;③空间四边形ABCD₁在正方体六个面内射影的面积的最小值为;④BE与CD₁所成的角为arcsin.

其中真命题的编号是          (写出所有真命题的编号).?

如图,正方体ABCD—A₁B₁C₁D₁的棱长为1,E为A₁B₁的中点,则下列五个命题:

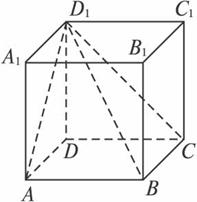
①点E到平面ABC₁D₁的距离为;

②直线BC与平面ABC₁D₁所成的角等于45°;

③空间四边形ABCD₁在正方体六个面内的射影围成的图形中,面积最小的值为;

④BE与CD₁所成角为arcsin;

⑤二面角ABD₁C的大小为.

其中真命题是.(写出所有真命题的序号)

如图，四棱锥P-ABCD中，底面ABCD是边长为2的正方形，PB⊥BC，PD⊥CD，且PA=2，E为PD中点．
（Ⅰ）求证：PA⊥平面ABCD；
（Ⅱ）求二面角E-AC-D的大小；
（Ⅲ）在线段BC上是否存在点F，使得点E到平面PAF的距离为？若存在，确定点F的位置；若不存在，请说明理由．