用数学归纳法证明：

．

【解析】首先证明当n=1时等式成立，再假设n=k时等式成立，得到等式

，

下面证明当n=k+1时等式左边

，

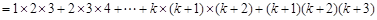根据前面的假设化简即可得到结果，最后得到结论．

 

已知基本不等式：≥（a、b都是正实数，当且仅当a=b时等号成立）可以推广到n个正实数的情况，即对于n个正实数a₁，a₂，a₃，…，a_n，有≥（当且仅当a₁=a₂=a₃=…=a_n时，取等号）.

    同理，当a、b都是正实数时，（a+b）（+）≥2ab·2·=4，可以推导出结论：对于n个正实数a₁，a₂，a₃，…，a_n有（a₁+a₂+a₃）（++）≥_______；（a₁+a₂+a₃+a₄）（+++）≥________；（a₁+a₂+a₃+…+a_n）（+++···）≥________；

    如果对于n个同号实数a₁，a₂，a₃，…，a_n（同正或者同负），那么，根据上述结论，（a₁+a₂+a₃+…+a_n）（+++···）的取值范围是________.

   

设数列{a_n}满足a₁=2,a_n+1=2a_n+2,用数学归纳法证明a_n=4×2^n-1-2的第二步中,设n=k时结论成立,即a_k=4×2^k-1-2,那么当n=k+1时, __________.

设数列{a_n}满足a₁=2,a_n+1=2a_n+2,用数学归纳法证明a_n=4×2^n-1-2的第二步中,设n=k时结论成立,即a_k=4×2^k-1-2,那么当n=k+1时, __________.