
题目列表(包括答案和解析)
-1±
| ||
| 4 |
-1+
| ||
| 4 |
-1-
| ||
| 4 |
-1+
| ||
| 4 |
化简![]() -
-![]() 得( )
得( )
A.6 B.2x
C.6或-2x D.-2x或6或2
-1±
| ||
| 4 |
-1+
| ||
| 4 |
-1-
| ||
| 4 |
-1+
| ||
| 4 |
已知 ,且
,且 .
.
(1)求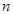 的值;
的值;
(2)求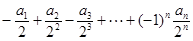 的值.
的值.
【解析】本试题主要考查了二项式定理的运用,以及系数求和的赋值思想的运用。第一问中,因为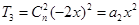 ,所以
,所以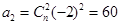 ,可得
,可得 ,第二问中,因为
,第二问中,因为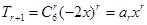 ,所以
,所以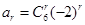 ,所以
,所以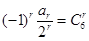 ,利用组合数性质可知。
,利用组合数性质可知。
解:(1)因为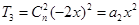 ,所以
,所以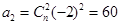 , ……3分
, ……3分
化简可得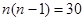 ,且
,且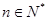 ,解得
,解得 . …………6分
. …………6分
(2)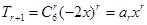 ,所以
,所以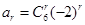 ,
,
所以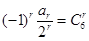 ,
,
| n |
| n |
一、1.D 2. B 3.A 4.D 5. D 6. A 7. B 8. C 9. D 10. C 11. C 12 A 13. 提示:此题为抽样方法的选取问题.当总体中个体较多时宜采用系统抽样;当总体中的个体差异较大时,宜采用分层抽样;当总体中个体较少时,宜采用随机抽样.
依据题意,第①项调查应采用分层抽样法、第②项调查应采用简单随机抽样法.故选B.
答案:B
|