
题目列表(包括答案和解析)
为了让更多的人参与2011年在深圳举办的“大运会”,深圳某旅游公司向国内外发行总量为2000万张的旅游优惠卡,其中向境外人士发行的是旅游金卡(简称金卡),向境内人士发行的是旅游银卡(简称银卡).现有一个由36名游客组成的旅游团到深圳参观旅游,其中![]() 是境外游客,其余是境内游客.在境外游客中有
是境外游客,其余是境内游客.在境外游客中有![]() 持金卡,在境内游客中有
持金卡,在境内游客中有![]() 持银卡.
持银卡.
(Ⅰ)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(Ⅱ)在该团的省内游客中随机采访3名游客,设其中持银卡人数为随机变量X,求X的分布列及数学期望EX.
某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为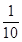 和p.
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为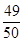 ,求p的值;
,求p的值;
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为 和p.
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为 ,求p的值;
,求p的值;
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
 和p.
和p. ,求p的值;
,求p的值;某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为![]() 和p.
和p.
(Ⅰ)若在任意时刻至少有一个系统不发生故障的概率为![]() ,求p的值;
,求p的值;
(Ⅱ)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
一、1.D 2. B 3.A 4.D 5. D 6. A 7. B 8. C 9. D 10. C 11. C 12 A 13. 提示:此题为抽样方法的选取问题.当总体中个体较多时宜采用系统抽样;当总体中的个体差异较大时,宜采用分层抽样;当总体中个体较少时,宜采用随机抽样.
依据题意,第①项调查应采用分层抽样法、第②项调查应采用简单随机抽样法.故选B.
答案:B
|