
题目列表(包括答案和解析)

| 1.04 |
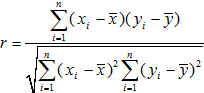
 |
| y |
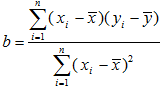 ,a=
,a=| y |
| x |
某班主任对全班50名学生进行迟到与学习成绩是否有关的调查,数据如下表:
|
(本小题满分15分)某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限 | 3 | 5 | 6 | 7 | 9 |
| 推销金额 | 2 | 3 | 3 | 4 | 5 |
(Ⅰ)求年推销金额![]() 与工作年限x之间的相关系数;(Ⅱ)求年推销金额
与工作年限x之间的相关系数;(Ⅱ)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;(Ⅲ)若第6名推销员的工作年限为11年,试估计他的年推销金额.(参考数据:;由检验水平0.01及
的线性回归方程;(Ⅲ)若第6名推销员的工作年限为11年,试估计他的年推销金额.(参考数据:;由检验水平0.01及![]() ,查表得
,查表得![]() .)
.)
| 学习成绩前26名 | 学习成绩后24名 | 总数 | |
| 从不迟到的 | 18 | 9 | 27 |
| 有过迟到的 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
| 50×(18×15-8×9)2 |
| 27×23×24×26 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A.97.5% | B.95% | C.90% | D.无充分根据 |

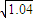 ≈1.02;由检验水平0.01及n-2=3,查表得r0.01=0.959.)
≈1.02;由检验水平0.01及n-2=3,查表得r0.01=0.959.)
 =bx+a,其中
=bx+a,其中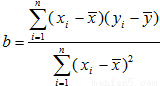 ,a=
,a=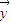 -b
-b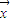 .
.一、1.D 2. B 3.A 4.D 5. D 6. A 7. B 8. C 9. D 10. C 11. C 12 A 13. 提示:此题为抽样方法的选取问题.当总体中个体较多时宜采用系统抽样;当总体中的个体差异较大时,宜采用分层抽样;当总体中个体较少时,宜采用随机抽样.
依据题意,第①项调查应采用分层抽样法、第②项调查应采用简单随机抽样法.故选B.
答案:B
|