
题目列表(包括答案和解析)
下列说法:[来源:学.科.网Z.X.X.K]
①从匀速传递的产品生产流水线上,质检员第10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样[来源:]
②某地气象局预报:5月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学
③在回归分析模型中,残差平方和越小,说明模型的拟合效果越好
④在回归直线方程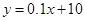 中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位
中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位
其中正确的是 (填上你认为正确的序号)
(本题满分15分)
已知函数 ,
, (
(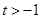 ),函数
),函数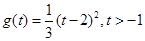 [来源:学.科.网]
[来源:学.科.网]
(Ⅰ)当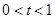 时,求函数
时,求函数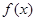 的单调区间和最大、最小值;
的单调区间和最大、最小值;
(Ⅱ)求证:对于任意的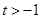 ,总存在
,总存在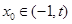 ,使得
,使得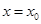 是关于
是关于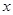 的方程
的方程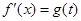 的解;并就
的解;并就 的取值情况讨论这样的
的取值情况讨论这样的 的个数。
的个数。
设函数f(x)=lnx,g(x)=ax+ ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.[来源:学。科。网]
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.[来源:学。科。网]
(Ⅰ)求a、b的值;
(Ⅱ)设x>0,试比较f(x)与g(x)的大小.[来源:学,科,网Z,X,X,K]
【解析】第一问解:因为f(x)=lnx,g(x)=ax+
则其导数为
由题意得,
第二问,由(I)可知 ,令
,令 。
。
∵ , …………8分
, …………8分
∴ 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当 时,
时, ,有
,有 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时, ,有
,有
解:因为f(x)=lnx,g(x)=ax+
则其导数为
由题意得,
(11)由(I)可知 ,令
,令 。
。
∵ , …………8分
, …………8分
∴ 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当 时,
时, ,有
,有 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时, ,有
,有
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com