
题目列表(包括答案和解析)
若对任意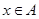 ,
,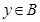 ,(
,(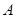 、
、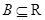 )有唯一确定的
)有唯一确定的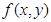 与之对应,称
与之对应,称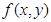 为关于
为关于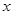 、
、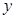 的二元函数. 现定义满足下列性质的二元函数
的二元函数. 现定义满足下列性质的二元函数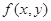 为关于实数
为关于实数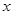 、
、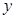 的广义“距离”:
的广义“距离”:
(1)非负性: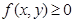 ,当且仅当
,当且仅当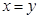 时取等号;
时取等号;
(2)对称性: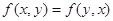 ;
;
(3)三角形不等式: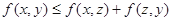 对任意的实数z均成立.
对任意的实数z均成立.
今给出个二元函数:①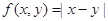 ;②
;②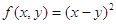 ;③
;③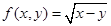 ;④
;④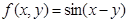 .则能够成为关于的
.则能够成为关于的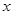 、
、 的广义“距离”的函数的所有序号是
.
的广义“距离”的函数的所有序号是
.
若对任意![]() ,(
,(![]() )有唯一确定的
)有唯一确定的![]() 与之对应,则称
与之对应,则称![]() 为关于
为关于![]() 的二元函数。现定义满足下列性质的二元函数
的二元函数。现定义满足下列性质的二元函数![]() 为关于实数
为关于实数![]() 的广义“距离”:
的广义“距离”:
(1)非负性:![]() ,当且仅当
,当且仅当![]() 时取等号;
时取等号;
(2)对称性:![]() ;
;
(3)三角形不等式:![]() 对任意的实数
对任意的实数![]() 均成立.
均成立.
今给出三个二元函数,请选出所有能够成为关于![]() 的广义“距离”的序号:
的广义“距离”的序号:
①![]() ;②
;②![]() ;③
;③![]() ._________________.
._________________.
设函数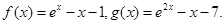
解不等式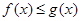 ;(4分)
;(4分)
事实上:对于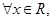 有
有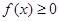 成立,当且仅当
成立,当且仅当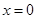 时取等号.由此结论证明:
时取等号.由此结论证明: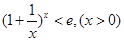 .(6分)
.(6分)
若对任意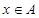 ,
,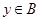 ,(
,(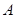 、
、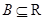 )有唯一确定的
)有唯一确定的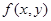 与之对应,称
与之对应,称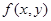 为关于
为关于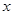 、
、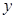 的二元函数.现定义满足下列性质的二元函数
的二元函数.现定义满足下列性质的二元函数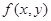 为关于实数
为关于实数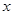 、
、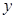 的广义“距离”:
的广义“距离”:
(1)非负性: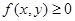 ,当且仅当
,当且仅当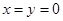 时取等号;
时取等号;
(2)对称性: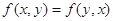 ;
;
(3)三角形不等式: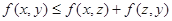 对任意的实数z均成立.
对任意的实数z均成立.
今给出四个二元函数:
①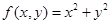 ;②
;②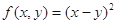 ③
③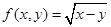 ;④
;④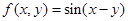 .
.
能够成为关于的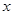 、
、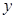 的广义“距离”的函数的所有序号是
.
的广义“距离”的函数的所有序号是
.
若对任意 ,
, ,(
,( 、
、 )有唯一确定的
)有唯一确定的 与之对应,称
与之对应,称 为关于
为关于 、
、 的二元函数. 现定义满足下列性质的二元函数
的二元函数. 现定义满足下列性质的二元函数 为关于实数
为关于实数 、
、 的广义“距离”:
的广义“距离”:
(1)非负性: ,当且仅当
,当且仅当 时取等号;
时取等号;
(2)对称性: ;
;
(3)三角形不等式: 对任意的实数z均成立.
对任意的实数z均成立.
今给出四个二元函数:① ;②
;② ③
③ ;
;
④ .
.
能够成为关于的 、
、 的广义“距离”的函数的所有序号是
.
的广义“距离”的函数的所有序号是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com