
题目列表(包括答案和解析)
已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点
的焦点![]() 重合,且椭圆短轴的两个端点与
重合,且椭圆短轴的两个端点与![]() 构成正三角形。
构成正三角形。
(Ⅰ)求椭圆的方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 与椭圆交于不同两点
与椭圆交于不同两点![]() ,试问在
,试问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使
,使![]() 恒为定值?若存在,求出
恒为定值?若存在,求出![]() 的坐标及定值;若不存在,请说明理由。
的坐标及定值;若不存在,请说明理由。
已知椭圆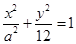 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,则该椭圆的离心率为( )
的焦点重合,则该椭圆的离心率为( )
A. B.
B.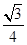 C.
C.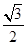 D.
D.
已知椭圆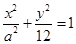 的一个焦点与抛物线
的一个焦点与抛物线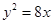 的焦点重合,则该椭圆的离心率为( )
的焦点重合,则该椭圆的离心率为( )
A.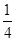 | B.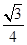 | C.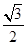 | D.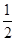 |
已知椭圆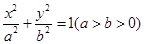 的一个焦点
的一个焦点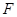 与抛物线
与抛物线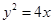 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为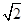 ,倾斜角为
,倾斜角为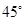 的直线
的直线 过点
过点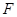 .
.
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为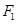 ,问抛物线
,问抛物线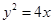 上是否存在一点
上是否存在一点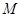 ,使得
,使得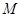 与
与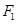 关于直线
关于直线 对称,若存在,求出点
对称,若存在,求出点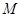 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
 的一个焦点
的一个焦点 与抛物线
与抛物线 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为
,倾斜角为 的直线
的直线 过点
过点 .
. ,问抛物线
,问抛物线 上是否存在一点
上是否存在一点 ,使得
,使得 与
与 关于直线
关于直线 对称,若存在,求出点
对称,若存在,求出点 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.一选择题
题号
1
2
3
4
5
6
7
8
9
10
答案
D
B
D
A
D
A
C
B
A
C
二、填空题
11.20 12.80 13.270 14.1 15.4884
三、解答题:
16.解:.files/image273.gif) .…………………4分
.…………………4分
(1)当.files/image170.gif) 时,
时,.files/image275.gif) ,
,
.files/image277.gif) 当
当.files/image279.gif) 时,
时,.files/image172.gif) 是增函数,
是增函数,
所以函数.files/image172.gif) 的单调递增区间为
的单调递增区间为.files/image281.gif) .…………8分
.…………8分
(2)由.files/image283.gif) 得
得.files/image285.gif) ,
, .files/image287.gif) .因为
.因为.files/image174.gif) ,
,
所以当.files/image289.gif) 时,
时,.files/image172.gif) 取最小值3,即
取最小值3,即.files/image291.gif) .当
.当.files/image293.gif) 时,
时,.files/image172.gif) 取最大值4,即
取最大值4,即.files/image295.gif) .将
.将.files/image295.gif) 代入得
代入得.files/image298.gif) . ……………13分
. ……………13分
17.解:(1)设袋中数学题的个数为.files/image300.gif)
则.files/image302.gif) …………2分
…………2分
化简得:.files/image304.gif) 又
又.files/image306.gif) ,即有5个数学题。…6分
,即有5个数学题。…6分
(2)由题知A、B、C、D,4个题中该生做 对2题,做错2题,其中:
A、B、C在三题中做对1个做错2个而D题做对的概率为:
.files/image308.gif) …………9分
…………9分
A、B、C三题中做对2个做错1个而D题做错的概率为:
.files/image310.gif) …………11分
…………11分
由互斥事件概率公式知所求概率为:
.files/image311.gif)
.files/image313.gif) …………13分
…………13分
18.(Ⅰ)取.files/image315.gif) 中点
中点.files/image317.gif) ,连结
,连结.files/image319.gif) .
.
.files/image321.gif) ,
,.files/image323.gif) . ………2分
. ………2分
.files/image325.gif) ,
,.files/image327.gif) .
.
.files/image329.gif) ,
,.files/image331.gif) 平面
平面.files/image333.gif) .…4分
.…4分
.files/image335.gif) 平面
平面.files/image333.gif) ,
,.files/image338.gif) .………6分
.………6分
(Ⅱ).files/image325.gif) ,
,.files/image341.gif) ,
,
.files/image343.gif) .
.
又.files/image198.gif) ,
,.files/image346.gif) .
.
.files/image347.gif) 又
又.files/image194.gif) ,即
,即.files/image350.gif) ,且
,且.files/image352.gif) ,
,
.files/image354.gif) 平面
平面.files/image356.gif) .
………8分
.
………8分
取.files/image358.gif) 中点
中点.files/image360.gif) .连结
.连结.files/image362.gif) .
.
.files/image364.gif) ,
,.files/image366.gif) .
.
.files/image368.gif) 是
是.files/image370.gif) 在平面
在平面.files/image356.gif) 内的射影,
内的射影,
.files/image373.gif) .
.
.files/image375.gif) 是二面角
是二面角.files/image202.gif) 的平面角.………10分
的平面角.………10分
在.files/image378.gif) 中,
中,.files/image380.gif) ,
,.files/image382.gif) ,
,.files/image384.gif) ,
,
.files/image386.gif) .
..files/image388.gif) 二面角
二面角.files/image202.gif) 的大小为
的大小为.files/image391.gif) .………13分
.………13分
19.解:(Ⅰ)由题意:.files/image393.gif) ∴
∴.files/image214.gif) ……………2分
……………2分
(Ⅱ)由(Ⅰ)知:.files/image396.gif)
.files/image398.gif)
数列.files/image220.gif) 满足:
满足:.files/image401.gif) ,故
,故.files/image403.gif) ……………6分
……………6分
(Ⅲ)令.files/image405.gif)
.files/image407.gif) ………8分
………8分
相减得:.files/image409.gif)
.files/image411.gif) ………10分
………10分
∴.files/image413.gif) ……………12分
……………12分
20.解析:(1).files/image415.gif) ………2分
………2分
.files/image417.gif)
.files/image419.gif) ………4分
………4分
当x≥1时,.files/image421.gif) 是增函数,其最小值为
是增函数,其最小值为.files/image423.gif)
.files/image425.gif) ………6分
………6分
(2)方程为.files/image427.gif) 令
令.files/image429.gif)
.files/image431.gif)
.files/image433.gif)
x
.files/image435.gif)
.files/image437.gif)
.files/image439.gif)
a
.files/image441.gif)
.files/image443.gif)
+
0
-
0
+
.files/image053.gif)
.files/image445.gif)
.files/image447.gif)
.files/image448.gif)
.files/image450.gif)
.files/image451.gif)
.files/image453.gif) 有极大值
有极大值.files/image455.gif)
.files/image457.gif) 有极小值,
有极小值,.files/image459.gif)
.files/image461.gif) ………8分
………8分
∵若方程f(x)=(.files/image229.gif) (a>0)至多有两个解,∴f(a)≥0或f(
(a>0)至多有两个解,∴f(a)≥0或f(.files/image437.gif) )≤0, ……10分
)≤0, ……10分
∴.files/image450.gif) ≥0或
≥0或.files/image447.gif) ≤0 (舍) 解得0<a≤1.
………12分
≤0 (舍) 解得0<a≤1.
………12分
21. 解:(Ⅰ)设双曲线方程为.files/image463.gif) (
(.files/image465.gif) ,
,.files/image467.gif) ),
),
则.files/image469.gif) ,
,.files/image471.gif) ,∴
,∴.files/image473.gif) .------------------------(2分)
.------------------------(2分)
又.files/image475.gif) 在双曲线上,∴
在双曲线上,∴.files/image477.gif) .
.
联立①②③,解得.files/image479.gif) ,
,.files/image481.gif) .∴双曲线方程为
.∴双曲线方程为.files/image483.gif) .--------(4分)
.--------(4分)
注:对点M用第二定义,得.files/image485.gif) ,可简化计算.
,可简化计算.
(Ⅱ).files/image487.gif) ,设
,设.files/image489.gif) ,
,.files/image491.gif) ,m:
,m:.files/image493.gif) ,则
,则
由.files/image495.gif) ,得
,得.files/image497.gif) ,
,.files/image499.gif) .--------------------(6分)
.--------------------(6分)
由.files/image501.gif) ,得
,得.files/image503.gif) .
.
∴.files/image505.gif) ,
,.files/image507.gif) .
..files/image509.gif) .
.
由.files/image499.gif) ,
,.files/image512.gif) ,
,.files/image507.gif) ,---------------------(8分)
,---------------------(8分)
消去.files/image515.gif) ,
,.files/image517.gif) ,
,
得.files/image519.gif) .------------------------(9分)
.------------------------(9分)
∵.files/image521.gif) ,函数
,函数.files/image523.gif) 在
在.files/image525.gif) 上单调递增,
上单调递增,
∴.files/image527.gif) ,∴
,∴.files/image529.gif) .------------------------(10分)
.------------------------(10分)
又直线m与双曲线的两支相交,即方程.files/image503.gif) 两根同号,
两根同号,
∴.files/image532.gif) .------------------------------------------------(11分)
.------------------------------------------------(11分)
∴.files/image534.gif) ,故
,故.files/image536.gif) .------------------------(12分)
.------------------------(12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com