题目列表(包括答案和解析)
（本小题满分13分）
某次月考数学第Ⅰ卷共有8道选择题，每道选择题有4个选项，其中只有一个是正确的；评分标准为：“每题只有一个选项是正确的，选对得5分，不选或选错得0分。”某考生每道题都给出一个答案，已确定有5道题的答案是正确的，而其余3道题中，有一道题可判断出两个选项是错误的，有一道题可以判断出一个选项是错误的，还有一道题因不了解题意而乱猜，试求该考生：
（Ⅰ）得40分的概率；
（Ⅱ）得多少分的可能性最大？
（Ⅲ）所得分数
的数学期望。
（本小题满分13分）
某次月考数学第Ⅰ卷共有8道选择题，每道选择题有4个选项，其中只有一个是正确的；评分标准为：“每题只有一个选项是正确的，选对得5分，不选或选错得0分。”某考生每道题都给出一个答案，已确定有5道题的答案是正确的，而其余3道题中，有一道题可判断出两个选项是错误的，有一道题可以判断出一个选项是错误的，还有一道题因不了解题意而乱猜，试求该考生：
（Ⅰ）得40分的概率；
（Ⅱ）得多少分的可能性最大？
（Ⅲ）所得分数
的数学期望。
(本小题满分13分)
在一次数学考试中，共有10道选择题，每题均有四个选项，其中有且只有一个选项是正确的，评分标准规定：“每道题只选一个选项，答对得5分，不答或答错得零分”.某考生已确定有6道题是正确的，其余题目中：有两道题可判断两个选项是错误的，有一道可判断一个选项是错误的，还有一道因不理解题意只好乱猜，请求出该考生：
(Ⅰ)得50分的概率；
(Ⅱ)得40分的概率.www.www.zxxk.com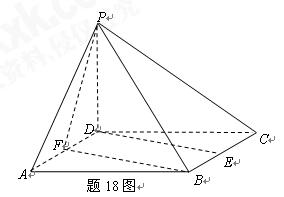
(本小题满分13分)
在一次数学考试中，共有10道选择题，每题均有四个选项，其中有且只有一个选项是正确
的，评分标准规定：“每道题只选一个选项，答对得5分，不答或答错得零分”.某考生已确定有6道题是正确的，其余题目中：有两道题可判断两个选项是错误的，有一道可判断一个选项是错误的，还有一道因不理解题意只好乱猜，请求出该考生：
(Ⅰ)得50分的概率；www.www.zxxk.com
(Ⅱ)设该考生所得分数为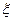
，求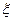的数学期望.
(本小题满分13分)
在一次数学考试中，共有10道选择题，每题均有四个选项，其中有且只有一个选项是正确的，评分标准规定：“每道题只选一个选项，答对得5分，不答或答错得零分”.某考生已确定有6道题是正确的，其余题目中：有两道题可判断两个选项是错误的，有一道可判断一个选项是错误的，还有一道因不理解题意只好乱猜，请求出该考生：
(Ⅰ)得50分的概率；
(Ⅱ)设该考生所得分数为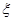
，求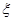的数学期望.
2009年4月
一、选择题：本大题共10小题，每题5分，共50分．
1．A 2．D 3．B 4．A 5．D 6．C 7．D 8．B 9．B 10．C
二、填空题：本大题共5小题，每题5分，共25分．
11．
12．
13．
14．
15．①②⑤
三、解答题：本题共6小题，共75分．
16．解：(1) 
??????????????????????????????????????? 3分
∴ 
∵ 
∴ 
??????????????????????????????????????????????????????????????????????????? 5分
∴ 
(2) 
????????????????????????????????????????????????????? 8分
∴ 
????????????????????????????????????????????????????????????????? 9分
∴ 
???????????????????????????????????????????????????????????????????? 10分
∴ 
?????????????????????????????????????????????????????????????????????????? 11分
∴ 
?????????????? 13分
17．解：(1) 有两道题答对的概率为
，有一道题答对的概率为
??????????????????????????? 2分
∴ 
????????????????????????????????????????????????????????? 5分
(2) 
?????????????????????????????????????????????????????? 7分
?????????????????????????????? 9分
??????????????????????????????? 11分
∴ 
的分布列为
35
40
45
50
P
???????????????????????????????????? 13分
18．(1) 证明：取CE中点M，则 FM
DE
∵ ABDE ∴ ABFM
∴ ABMF为平行四边形
∴ AF∥BM
又AF
平面BCE，BM
平面BCE
∴ AF∥平面BCE??????????????????????????????????????????????????????????????????? 4分
(2) 解：过C作l∥AB，则l∥DE ∴ 平面ABC
平面CDE = l
∵ AB⊥平面ACD ∴ l⊥平面ACD
∴ ∠ACD即为所求二面角的平面角，为60
?????????????????????????????????? 8分
(3) 解：设B在平面AFE内的射影为
，作MN⊥FE于N，作CG⊥EF于G．
∴ BE与平面AFE所成角为
∵ AF⊥CD，AF⊥DE ∴ AF⊥平面CDE ∴ AF⊥MN ∴ MN⊥平面AEF
∵ BM∥平面AEF ∴ 
由△CGF∽△EDF，得
∴ 
而 
∴ 
∴ 
???????????????????????????????????????????????????????????????? 13分
19．解：(1) 
?????????????????????????????????????????????????????????????????????????? 2分
由
由
∴ 
上单调递减，在
上单调递增????????????????????????? 5分
(2) 
?????????????????????????????????????????? 6分
∵ 上递减 ∴ 
??????????????? 9分
设
∵ 
∴
上递减
∴ 
即 
∴ 
???????????????????????????????????????????????????????????????????????? 12分
20．解：(1) B（0，? b），A（
，0），F（c，0），P（c，
）
∵ 
∴ D为线段FP的中点，
∴ D为（c，
）??????????????????????????????????????????????????????????????????? 2分
∴ 
，∴ a = 2b，
∴ 
?????????????????????????????????????????????? 5分
(2) a = 2，则b = 1，B（0，?1） 双曲线的方程为
①
设M（x1，y1），N（x2，y2），C（0，m）
由
由已知
???????????????????????????? 7分
设
整理得：
对满足
的k恒成立
∴ 
．
故存在y轴上的点C（0，4），使
为常数17．????????????????????? 12分
21．解：(1) 
???????????????????????????????????????????????????????????????????????????? 1分
切线方程为
与y = kx联立得：
，令y = 0得：xB = 2t????????????????????????????????????????????????? 3分
∴ 
??????????????????????????????????????????????????????? 4分
(2) 由
??????????????????????????????????????????????????? 5分
两边取倒数得：
∴ 
∴ 
是以
为首项，为公比的等比数列（
时）
或是各项为0的常数列（k = 3时），此时an = 1
时
??????????????????????????????? 7分
当k = 3时也符合上式
∴
????????????????????????????????????????????????????????????????? 8分
(3) 作差得 
其中
由于 1 < k < 3，∴ 
∴ 
当
?????????????????????????????????????????????????? 12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com