
题目列表(包括答案和解析)
已知函数![]() 是
是![]() 上的偶函数,且
上的偶函数,且![]() ,当
,当![]() ,则函数
,则函数![]() 的零
的零
点个数 ( )
已知函数![]() 是
是![]() 上的偶函数,且
上的偶函数,且![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() = .
= .
已知函数 是
是 上的偶函数,对于
上的偶函数,对于 都有
都有 成立,且
成立,且 ,当
,当 且
且 时,都有
时,都有 ,则给出下列命题:
,则给出下列命题:
① ;②函数
;②函数 图象的一条对称轴为
图象的一条对称轴为 ;③函数
;③函数 在
在 上为减函数;④ 方程
上为减函数;④ 方程 在
在 上有4个根 ,上述命题中的所有正确命题的序号是 .(把你认为正确命题的序号都填上)
上有4个根 ,上述命题中的所有正确命题的序号是 .(把你认为正确命题的序号都填上)
已知函数 是
是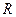 上的偶函数,对于
上的偶函数,对于 ,都有
,都有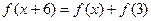 成立,当
成立,当 且
且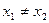 时,都有
时,都有 ,给出下列命题:
,给出下列命题:
①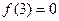 ;
;
②直线 是函数
是函数 的图象的一条对称轴;
的图象的一条对称轴;
③函数 在
在 上为增函数;④方程
上为增函数;④方程 在
在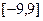 上有四个实根.
上有四个实根.
其中正确的命题序号是___________.(把所有正确命题的序号都填上)
已知函数 是
是 上的偶函数,且
上的偶函数,且 当
当 时,
时, ,则函数
,则函数 的零点个数是
的零点个数是
A.3 B.4 C.5 D.6
一、 C B C B B AC D A B C D
二、13.  14.
14.  15.
15.  16.3
16.3
三、17(Ⅰ)
= =
=
由 得,
得, 或
或

由 得
得  或
或 .
.
故函数 的零点为
的零点为 和
和 .
……………………………………6分
.
……………………………………6分
(Ⅱ)由
 ,
, 得
得 
由 得
得  .又
.又
由 得
得

 ,
,
 ……………………………………12分
……………………………………12分
18. 由三视图可知: ,底面ABCD为直角梯形,, BC=CD=1,AB=2
,底面ABCD为直角梯形,, BC=CD=1,AB=2
(Ⅰ)∵  PB⊥DA,梯形ABCD中,PB=BC=CD=1,AB=2 ∴BD=
PB⊥DA,梯形ABCD中,PB=BC=CD=1,AB=2 ∴BD=
又可得DA= ,∴DA⊥BD ,∴DA⊥平面PDB,
,∴DA⊥BD ,∴DA⊥平面PDB,
∴ AD⊥PD ……………………………4分
(Ⅱ) CM∥平面PDA 理由如下:
取PB中点N,连结MN,DN,可证MN∥CD且MN=CD,∴CM∥DN,∴CM∥平面PDA
…………8分
(Ⅲ) 
……………12分
19. (Ⅰ)九年级(1)班应抽取学生10名; ………………………2分
(Ⅱ)通过计算可得九(1)班抽取学生的平均成绩为16.5,九(2)班抽取学生的平均成绩为17.2.由此可以估计九(1)班学生的平均成绩为16.5, 九(2)班学生的平均成绩为 17.2 ………………………6分
(Ⅲ)基本事件总数为15,满足条件的事件数为9 ,故所求事件的概率为
………………………………12分
20. (Ⅰ)证明 设

相减得 
注意到 
有


即
 …………………………………………5分
…………………………………………5分
(Ⅱ)①设
由垂径定理,
即 
化简得 
当 与
与 轴平行时,
轴平行时, 的坐标也满足方程.
的坐标也满足方程.
故所求 的中点
的中点 的轨迹
的轨迹 的方程为
的方程为 ;
;
…………………………………………8分
②
假设过点P作直线 与有心圆锥曲线
与有心圆锥曲线 交于
交于 两点,且P为
两点,且P为 的中点,则
的中点,则

由于

直线 ,即
,即 ,代入曲线
,代入曲线 的方程得
的方程得


故这样的直线不存在. ……………………………………12分
21.(Ⅰ)函数的定义域为
 由题意易知,
由题意易知,  得
得  ;
;
 当
当 时,
时, 当
当 时,
时,
故函数 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为 . …………………………6分
. …………………………6分
(Ⅱ)
①
当 时,
时,
 在
在 递减,
递减, 无极值.
无极值.
②
当 时,由
时,由 得
得 

当 时,
时, 当
当 时,
时,
 时,函数
时,函数 的极大值为
的极大值为
 ;
;
函数 无极小值.
…………………………13分
无极小值.
…………………………13分
22.(Ⅰ)

 …………………………………………4分
…………………………………………4分
(Ⅱ) ,
,
 ……………………………8分
……………………………8分
(Ⅲ)假设

记 ,可求
,可求

故存在 ,使
,使 恒成立.
恒成立.
……………………………………13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com