
题目列表(包括答案和解析)
不等式选讲选做题
已知函数f(x)=|x+1|||x-2|,不等式t≤f(x)在R上恒成立.
(Ⅰ)求t的取值范围;
(Ⅱ)记t的最大值为T,若正实数a,b,c满足a2+b2+c2=T,求a+2b+c的最大值.
(不等式选讲选做题)函数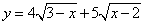 的最大值为
,取得最大值时
的最大值为
,取得最大值时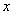 的值为
的值为
[选做题]
A.选修4—1:几何证明选讲
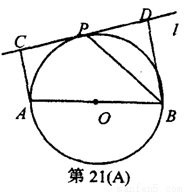
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.
|
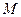 对应的变换将点
对应的变换将点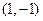 与
与 分别变换成点
分别变换成点 与
与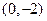 .求矩阵
.求矩阵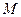 ;
;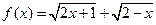 的最大值.
的最大值.[选做题]
A.选修4—1:几何证明选讲
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.
B.选修4—2:矩阵与变换
二阶矩阵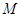 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点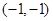 与
与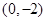 .求矩阵
.求矩阵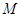 ;
;
C.选修4—4:坐标系与参数方程
若两条曲线的极坐标方程分别为=l与=2cos(θ+),它们相交于A,B两点,求线
段AB的长.
D.选修4—5:不等式选讲
求函数 的最大值.
的最大值.

|
 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .求矩阵
.求矩阵 ;
; 的最大值.
的最大值.一.选择题:BAAC ADBC
解析:
1.2009.4.files/image214.gif) ,复数
,复数 2009.4.files/image002.gif) 对应的点为
对应的点为2009.4.files/image216.gif) ,它与原点的距离是
,它与原点的距离是2009.4.files/image006.gif) ,故选B.
,故选B.
2.2009.4.files/image016.gif)
2009.4.files/image218.gif) ,但
,但2009.4.files/image018.gif)
2009.4.files/image220.gif)
2009.4.files/image016.gif) .故选A.
.故选A.
3.∵2009.4.files/image020.gif) 是等差数列,
是等差数列,2009.4.files/image022.gif) ,
,2009.4.files/image024.gif) ,∴
,∴2009.4.files/image222.gif) ,
,2009.4.files/image224.gif) ,
,
∴2009.4.files/image226.gif) ,故选A.
,故选A.
4.依题意知,2009.4.files/image228.gif) ,
,2009.4.files/image230.gif) ,又
,又2009.4.files/image232.gif) ,
,2009.4.files/image234.gif) ,
,2009.4.files/image236.gif) ,
,2009.4.files/image238.gif) ,故选C.
,故选C.
2009.4.files/image240.gif) 5.把直线
5.把直线2009.4.files/image047.gif) 向下平移二个单位,则点
向下平移二个单位,则点2009.4.files/image045.gif) 到直线
到直线2009.4.files/image242.gif) 的距离就相等了,故点
的距离就相等了,故点2009.4.files/image045.gif) 的轨迹为抛物线,它的方程为
的轨迹为抛物线,它的方程为2009.4.files/image052.gif) ,选A.
,选A.
6.由三视图知该工作台是棱长为802009.4.files/image244.gif) 的正方体上面围上一块矩形和两块直角三角形合
的正方体上面围上一块矩形和两块直角三角形合
板,如右图示,则用去的合板的面积2009.4.files/image246.gif) 故选D.
故选D.
7.2009.4.files/image248.gif) ,
,2009.4.files/image250.gif) ,故选B.
,故选B.
2009.4.files/image252.gif) 8.由
8.由2009.4.files/image094.gif) ,可得:
,可得:2009.4.files/image255.gif) 知满足事件A的区域的面积
知满足事件A的区域的面积
2009.4.files/image257.gif) ,而满足所有条件的区域
,而满足所有条件的区域2009.4.files/image259.gif) 的面积:
的面积:2009.4.files/image261.gif) ,从而,
,从而,
得:2009.4.files/image263.gif) ,故选C.
,故选C.
二.填空题:9.18 ; 10.2;11. 2009.4.files/image265.gif) ;12.
;12. 2009.4.files/image267.gif) 、
、2009.4.files/image269.gif) ;13.
;13. 2009.4.files/image271.gif) ;14.
;14.2009.4.files/image273.gif) ;15.
;15.2009.4.files/image086.gif) 、
、2009.4.files/image084.gif)
解析:9.按系统抽样的方法,样本中4位学生的座位号应成等差数列,将4位学生的座位号按从小到大排列,显然6,30不可能相邻,也就是中间插有另一位同学,其座位号为(6+30)÷2=18,故另一位同学的座位号为18.
10. 2009.4.files/image277.gif) ,令
,令2009.4.files/image279.gif)
从而展开式中2009.4.files/image108.gif) 的系数是
的系数是2009.4.files/image281.gif) ,故填2.
,故填2.
11.2009.4.files/image283.gif)
2009.4.files/image285.gif)
2009.4.files/image287.jpg)
2009.4.files/image289.gif) ,故填
,故填2009.4.files/image265.gif) .
.
12.设人经过时间ts后到达点B,这时影长为AB=S,如图由平几的
知识可得2009.4.files/image291.gif) ,
,2009.4.files/image293.gif) =
=2009.4.files/image295.gif) ,由导数的意义知人影长度
,由导数的意义知人影长度
的变化速度v=2009.4.files/image297.gif) (m/s)
(m/s)
2009.4.files/image299.gif) 13.曲线
13.曲线2009.4.files/image116.gif) 为抛物线段
为抛物线段2009.4.files/image301.gif) 借助图形直观易得
借助图形直观易得2009.4.files/image271.gif)
14. 2009.4.files/image303.gif) ,由柯西不等式得:
,由柯西不等式得:2009.4.files/image305.gif)
2009.4.files/image307.gif) ∴
∴2009.4.files/image309.gif)
2009.4.files/image311.gif) .
.2009.4.files/image313.gif)
15.由切割线定理得2009.4.files/image315.gif) ,
,2009.4.files/image317.gif) ,
,
连结OC,则2009.4.files/image319.gif) ,
,2009.4.files/image321.gif) ,
,2009.4.files/image323.gif)
三.解答题:
16.解:(1)2009.4.files/image128.gif)
2009.4.files/image326.gif)
2009.4.files/image328.gif) ---3分
---3分
∴函数的最小正周期为2009.4.files/image330.gif) ,值域为
,值域为2009.4.files/image332.gif) 。--------------------------------------5分
。--------------------------------------5分
(2)解法1:依题意得:2009.4.files/image334.gif)
2009.4.files/image336.gif) ---------------------------6分
---------------------------6分
∵2009.4.files/image338.gif) ∴
∴2009.4.files/image340.gif)
∴2009.4.files/image342.gif) =
=2009.4.files/image344.gif) -----------------------------------------8分
-----------------------------------------8分
2009.4.files/image135.gif) =
=2009.4.files/image346.gif)
∵2009.4.files/image348.gif) =
=2009.4.files/image350.gif)
∴2009.4.files/image135.gif) =
=2009.4.files/image352.gif) ------------------------------------------------------------------------------12分
------------------------------------------------------------------------------12分
解法2:依题意得: 2009.4.files/image336.gif) 得
得2009.4.files/image354.gif) ----①-----------7分
----①-----------7分
∵2009.4.files/image338.gif) ∴
∴2009.4.files/image340.gif)
∴2009.4.files/image342.gif) =
=2009.4.files/image344.gif) ---------------------------------9分
---------------------------------9分
由2009.4.files/image342.gif) =
=2009.4.files/image356.gif) 得
得2009.4.files/image358.gif) -----------②----------------10分
-----------②----------------10分
①+②得2009.4.files/image360.gif) ,∴
,∴2009.4.files/image135.gif) =
=2009.4.files/image352.gif) -------------------------12分
-------------------------12分
解法3:由2009.4.files/image363.gif) 得
得2009.4.files/image354.gif) ,--------------------7分
,--------------------7分
两边平方得2009.4.files/image365.gif)
2009.4.files/image367.gif) ,
,2009.4.files/image369.gif) ,--------------------------8分
,--------------------------8分
∵2009.4.files/image338.gif) ∴
∴2009.4.files/image371.gif) 由
由2009.4.files/image369.gif)
2009.4.files/image373.gif) 知
知2009.4.files/image375.gif)
∴2009.4.files/image377.gif) --------------------------------------9分
--------------------------------------9分
由2009.4.files/image379.gif) ,得
,得2009.4.files/image381.gif) --------------------10分
--------------------10分
∴2009.4.files/image383.gif) ∴
∴2009.4.files/image135.gif) =
=2009.4.files/image352.gif) .---------------------------------12分
.---------------------------------12分
17.解:(1)不论点2009.4.files/image045.gif) 在
在2009.4.files/image146.gif) 上的任何位置,都有平面
上的任何位置,都有平面2009.4.files/image148.gif) 垂直于平面
垂直于平面2009.4.files/image150.gif) .---1分
.---1分
证明如下:由题意知,2009.4.files/image385.gif) ,
,2009.4.files/image387.gif)
又2009.4.files/image389.gif)
2009.4.files/image391.gif) 平面
平面2009.4.files/image150.gif)
又2009.4.files/image393.gif) 平面
平面2009.4.files/image148.gif)
2009.4.files/image395.gif) 平面
平面2009.4.files/image148.gif)
2009.4.files/image126.gif) 平面
平面2009.4.files/image150.gif) .------------------4分
.------------------4分
(2)解法一:过点P作2009.4.files/image398.gif) ,垂足为
,垂足为2009.4.files/image400.gif) ,连结
,连结2009.4.files/image402.gif) (如图),则
(如图),则2009.4.files/image404.gif) ,
,
2009.4.files/image406.gif) 是异面直线
是异面直线2009.4.files/image152.gif) 与
与2009.4.files/image154.gif) 所成的角.----------------------6分
所成的角.----------------------6分
2009.4.files/image408.gif) 在
在2009.4.files/image410.gif) 中 ∵
中 ∵2009.4.files/image141.gif) ∴
∴2009.4.files/image412.gif)
∴2009.4.files/image414.gif) ,
, 2009.4.files/image416.gif) ,
,
2009.4.files/image418.gif) .
.
又2009.4.files/image420.gif) .
.
2009.4.files/image395.gif) 在
在2009.4.files/image423.gif) 中,
中,2009.4.files/image425.gif)
2009.4.files/image427.gif) .----------8分
.----------8分
2009.4.files/image395.gif) 异面异面直线
异面异面直线2009.4.files/image152.gif) 与
与2009.4.files/image154.gif) 所成角的余弦值为
所成角的余弦值为2009.4.files/image430.gif) .----------------9分
.----------------9分
2009.4.files/image432.gif) 解法二:以
解法二:以2009.4.files/image434.gif) 为原点,
为原点,2009.4.files/image436.gif) 所在的直线为x轴建立空间直角坐标系如图示,则
所在的直线为x轴建立空间直角坐标系如图示,则2009.4.files/image438.gif) ,
,2009.4.files/image440.gif) ,
,2009.4.files/image442.gif) ,
,2009.4.files/image444.gif) ,
,2009.4.files/image446.gif) ,
,
2009.4.files/image448.gif) -----6分
-----6分
∴2009.4.files/image450.gif)
2009.4.files/image452.gif) .
.
∴异面异面直线2009.4.files/image152.gif) 与
与2009.4.files/image154.gif) 所成角的余弦值为
所成角的余弦值为2009.4.files/image430.gif) .-----9分
.-----9分
(3)由(1)知,2009.4.files/image454.gif) 平面
平面2009.4.files/image150.gif) ,
,
2009.4.files/image456.gif) 是
是2009.4.files/image156.gif) 与平面
与平面2009.4.files/image150.gif) 所成的角,---------------------------10分
所成的角,---------------------------10分
且2009.4.files/image458.gif) .------------------------------------11分
.------------------------------------11分
当2009.4.files/image460.gif) 最小时,
最小时,2009.4.files/image462.gif) 最大,这时
最大,这时2009.4.files/image464.gif) ,由
,由2009.4.files/image466.gif) --13分
--13分
得2009.4.files/image468.gif) ,即
,即2009.4.files/image156.gif) 与平面
与平面2009.4.files/image150.gif) 所成角的正切值的最大值
所成角的正切值的最大值2009.4.files/image470.gif) .---14分
.---14分
18.解: 用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,
且2009.4.files/image472.gif) .------------------------------------------------------2分
.------------------------------------------------------2分2009.4.files/image313.gif)
(1)至少有1人面试合格的概率是
2009.4.files/image475.gif) ----------------------4分
----------------------4分
(2)2009.4.files/image477.gif) 的可能取值为0,1,2,3.----------------------------------------------------------5分
的可能取值为0,1,2,3.----------------------------------------------------------5分
∵ 2009.4.files/image479.gif)
=2009.4.files/image481.gif)
=2009.4.files/image483.gif) ---------------------------6分
---------------------------6分
2009.4.files/image485.gif)
=2009.4.files/image487.gif)
=2009.4.files/image489.gif) --------------------------------7分
--------------------------------7分
2009.4.files/image491.gif) ---------------------8分
---------------------8分
2009.4.files/image493.gif) ----------------------9分
----------------------9分
∴2009.4.files/image477.gif) 的分布列是
的分布列是
2009.4.files/image477.gif)
0
1
2
3
2009.4.files/image496.gif)
2009.4.files/image498.gif)
2009.4.files/image498.gif)
2009.4.files/image500.gif)
2009.4.files/image500.gif)
-------------10分
2009.4.files/image477.gif) 的期望
的期望2009.4.files/image502.gif) ----------------------------------------12分
----------------------------------------12分
19.解:(1)当2009.4.files/image169.gif)
2009.4.files/image313.gif) 时,∵
时,∵2009.4.files/image505.gif) ,∴
,∴2009.4.files/image507.gif) ,
,
∴2009.4.files/image509.gif) ,
,2009.4.files/image511.gif)
2009.4.files/image100.gif) ,点
,点2009.4.files/image514.gif) ,
,2009.4.files/image516.gif) ,
,2009.4.files/image518.gif) ------------2分
------------2分
2009.4.files/image520.gif) 设
设2009.4.files/image165.gif) 的方程为
的方程为2009.4.files/image522.gif)
由2009.4.files/image165.gif) 过点F,B,C得
过点F,B,C得
∴2009.4.files/image524.gif) -----------------①
-----------------①
2009.4.files/image526.gif) -----------------②
-----------------②
2009.4.files/image528.gif) -------------------③----------------------------5分
-------------------③----------------------------5分
由①②③联立解得2009.4.files/image530.gif)
2009.4.files/image532.gif) ,
,2009.4.files/image534.gif) ,
,2009.4.files/image536.gif) -----------------------7分
-----------------------7分
∴所求的2009.4.files/image165.gif) 的方程为
的方程为2009.4.files/image538.gif) -------------8分
-------------8分
(2)∵2009.4.files/image165.gif) 过点F,B,C三点,∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,FC的垂直平分线方程为
过点F,B,C三点,∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,FC的垂直平分线方程为2009.4.files/image540.gif) --------④----------------------9分
--------④----------------------9分
∵BC的中点为2009.4.files/image542.gif) ,
,2009.4.files/image544.gif)
∴BC的垂直平分线方程为2009.4.files/image546.gif) -----⑤---------------------10分
-----⑤---------------------10分
由④⑤得2009.4.files/image548.gif) ,即
,即2009.4.files/image550.gif) ----------------11分
----------------11分
∵P2009.4.files/image167.gif) 在直线
在直线2009.4.files/image171.gif) 上,∴
上,∴2009.4.files/image552.gif)
2009.4.files/image554.gif)
2009.4.files/image556.gif)
∵2009.4.files/image558.gif) ∴
∴2009.4.files/image560.gif)
由2009.4.files/image562.gif) 得
得2009.4.files/image564.gif) -------------------------------------------13分
-------------------------------------------13分
∴椭圆的方程为2009.4.files/image566.gif) --------------------------------------------------------------14分
--------------------------------------------------------------14分
20.解:(1)当
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com