
题目列表(包括答案和解析)
(19)(本小题满分12分)
为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物。某人一次种植了n株沙柳,各株沙柳成活与否是相互独立的,成活率为p,设![]() 为成活沙柳的株数,数学期望
为成活沙柳的株数,数学期望![]() ,标准差
,标准差![]() 为
为![]() 。
。
(Ⅰ)求n,p的值并写出![]() 的分布列;
的分布列;
(Ⅱ)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率
19(本小题满分12分)
P是以![]() 为焦点的双曲线C:
为焦点的双曲线C:![]() (a>0,b>0)上的一点,已知
(a>0,b>0)上的一点,已知![]() =0,
=0,![]() .
.
(1)试求双曲线的离心率![]() ;
;
(2)过点P作直线分别与双曲线两渐近线相交于P1、P2两点,当![]() ,
,![]() = 0,求双曲线的方程.
= 0,求双曲线的方程.
(19) (本小题满分12分)某厂家根据以往的经验得到有关生产销售规律如下:每生产![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本2万元,每生产1百台需生产成本1万元(总成本
(万元),其中固定成本2万元,每生产1百台需生产成本1万元(总成本![]() 固定成本
固定成本![]() 生产成本);销售收入
生产成本);销售收入![]() (万元)满足:
(万元)满足: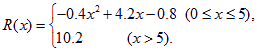 (Ⅰ)要使工厂有盈利,求
(Ⅰ)要使工厂有盈利,求![]() 的取值范围;
的取值范围;
(Ⅱ)求生产多少台时,盈利最多?
(本小题满分12分)
某初级中学有三个年级,各年级男、女生人数如下表:
| 初一年级 | 初二年级 | 初三年级 | |
| 女生 | 370 | z | 200 |
| 男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求z的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,将该样本看成一个总体,从中任选2名学生,求至少有1名女生的概率;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2, 1.5, 1.2, 1.5, 1.5, 1.3, 1.0, 1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
(本小题满分12分)
某初级中学共有学生2000名,各年级男、女生人数如下表:
| 初一年级 | 初二年级 | 初三年级 | |
| 女生 | 373 | x | Y |
| 男生 | 377 | 370 | z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19。 (I)求x的值; (II)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名? (III)已知![]() ,求初三年级中女生比男生多的概率。
,求初三年级中女生比男生多的概率。
一、 BCCC,ADBA
二、 30 2 1
1  50 96 96
50 96 96 
三、 解答题
16 (1) 


ω

(2)


17 (I)以D为原点,DA,DC,DD1所在直线为x轴,y轴,z轴,建立系
E点坐标为(1,1,1).
(2) 略
(3)二面角D1―BF―C的余弦值为
18
(1) 
(2)

(3)(Ⅰ)
当且仅当 时,即x=7时等号成立.
时,即x=7时等号成立.
 到第7年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.……10分
到第7年,年平均盈利额达到最大值,工厂共获利12×7+30=114万元.……10分
(Ⅱ)
故到第10年,盈利额达到最大值,工厂获利102+12=114万元 ……11分
盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理.…12分
19(1)椭圆 的方程是:
的方程是: .
.
(2) ,
, ,
,
 为常数.
为常数.
20 (1)用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,
至少有1人面试合格的概率是
(2)∴ 的分布列是
的分布列是

0
1
2
3





 的期望
的期望
21(1) (2)(2)①
(2)(2)①

 ,
, .
. 当
当 时,
时, . 假设
. 假设 ,则
,则 .
.
由数学归纳法证明 为常数数列,是等差数列,其通项为
为常数数列,是等差数列,其通项为 . ……8分
. ……8分
② ,
,  .
.
 当
当 时,
时, . 假设
. 假设 ,则
,则
 .
.
由数学归纳法,得出数列
 .……………10分
.……………10分
又 ,
, ,
,
即 ………12分
………12分



 .
.
 ,
, . ………………14分
. ………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com